【入門】アフィン変換のプログラミングに向けて【数値計算】

画像と同一形状の2次元配列に変換元座標配列を生成。

アフィン逆変換を一括でできるよう、
入力、出力の列ベクトルを拡張した形として行列にした。
これを再度、座標系の構成に直す。
イメージ的にはこんな感じ。

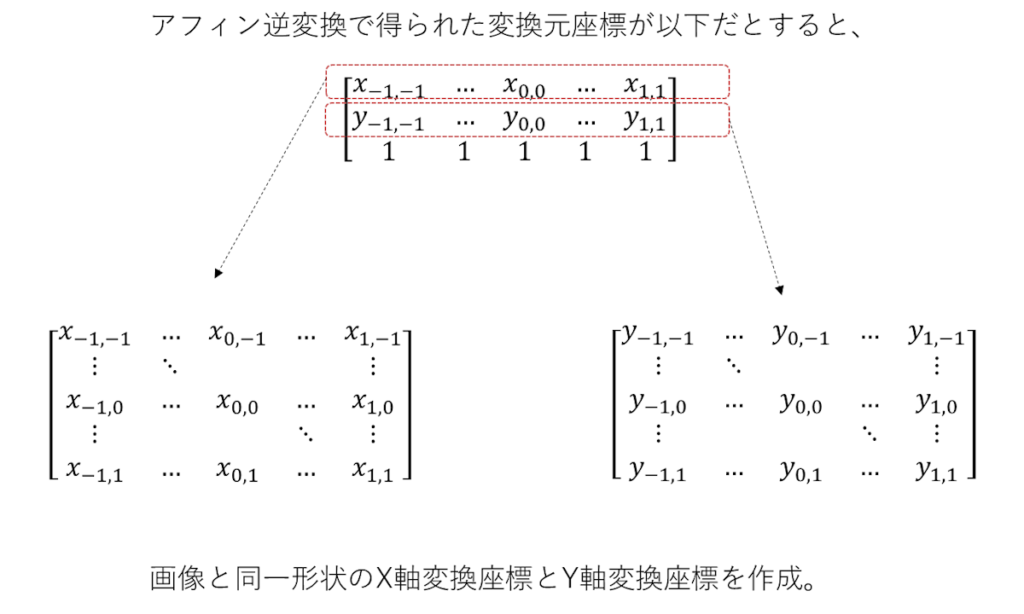
演算都合で1次元的にしたものを2次元平面に戻す作業になる。

次は、「変換元の座標系-1～1をピクセル位置に変換。」
これも変換都合で変形したものを再度元に戻す作業。
演算都合にしたものを描画都合に直してる。
イメージ的には以下になる。

そして、「元画像と変換元座標を元に変換先へコピー。」
変換座標の情報を元に実際のピクセルコピー作業だ。

アフィン変換で変換座標は求めてあったが、まだピクセルコピーはしていない。
これをここで実施する。

変換元から変換先にコピーだと、まだら模様問題が発生するので、
変換元から変換先を特定して、漏れなくコピーする方式だ。
処理イメージは以下になる。

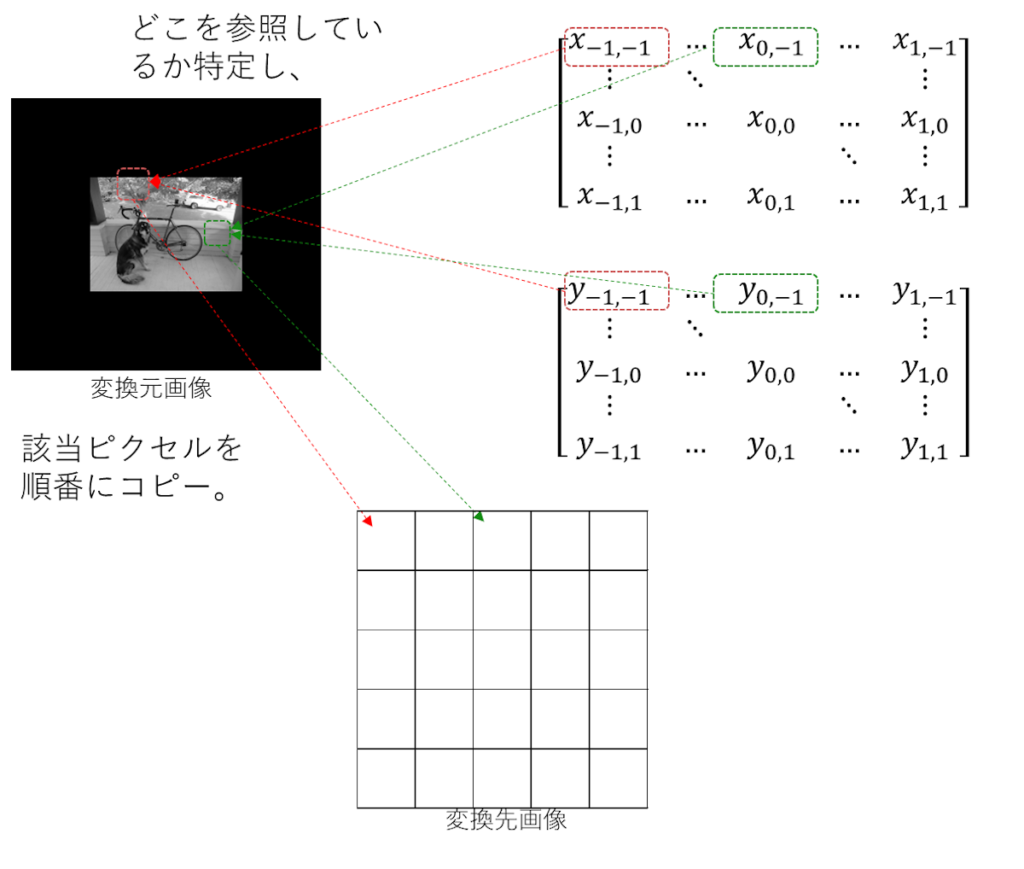
これができれば、各ピクセル情報が確定するから画像として扱える状態になる。

その後の画像保存は従来と一緒だから割愛する。

MATLAB、Python、Scilab、Julia比較ページはこちら