MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第3章 その94【射影変換⑧】
MATLAB,Python,Scilab,Julia比較 第3章 その95【射影変換⑨】
MATLAB,Python,Scilab,Julia比較 第3章 その96【射影変換⑩】
MATLAB,Python,Scilab,Julia比較 第3章 その97【射影変換⑪】
MATLAB,Python,Scilab,Julia比較 第3章 その98【射影変換⑫】
を書き直したもの。
アフィン変換の拡張と言われている射影変換の話。
射影変換の理屈について語っていく。
アフィン変換との関係性、係数の求め方、処理の流れについて
【再掲】射影変換の理屈の因果関係
まずは大まかな流れを再掲
- 大まかな理屈(済)
- 大まかな理屈を座標変換で説明(済)
- 基本ベクトルと基底ベクトル(済)
- 元画像平面を3次元空間で表現(済)
- 3次元空間を地面平面に落とし込む(済)
- 一連の座標変換まとめ(済)
- 方程式の変形(済)
- 行列表現(済)
- アフィン変換との関係性
- 係数の求め方
- 係数の求め方(行列表現)
- 射影変換の処理の流れ
「行列表現」というところまで終わっている。
アフィン変換との関係性
前回の行列表現を再掲しよう。
\(
s
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}=
\begin{bmatrix}
a&b&c\\
d&e&f\\
g&h&1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\)
この行列に見覚えが無いだろうか?
アフィン変換の酷似している。
射影変換の変換行列を\(g\)と\(h\)を\(0\)にすると
\(s=gx+hy+1\)の都合で\(s=1\)になる。
つまり、アフィン変換の変換行列と等しくなる。
アフィン変換
\(
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}=
\begin{bmatrix}
a&b&c\\
d&e&f\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\)
つまり、射影変換は数式的にはアフィン変換の拡張型と言える。
概念的には別物だが、結果的には拡張型になる。
係数の求め方
変換式は出たが、肝心の係数が求まる算段が付いていない。
結論としては連立方程式を利用する。
連立方程式にしやすいようにa~hの並びになるよう数式を変形する。
まずは元の式
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle sx\prime=\frac{ax+by+c}{s} \\
\displaystyle sy\prime=\frac{dx+ey+f}{s} \\
\displaystyle s=gx+hy+1
\end{array}
\right.
\end{eqnarray}
\)
これを変形して、
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
x\prime(gx+hy+1)=ax+by+c \\
y\prime(gx+hy+1)=dx+ey+f \\
\end{array}
\right.
\end{eqnarray}
\)
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by+c-gxx\prime-hyx\prime=x\prime \\
dx+ey+f-gxy\prime-hyy\prime=y\prime \\
\end{array}
\right.
\end{eqnarray}
\)
自明な数値
ここで、座標変換を考えた際に自明な数値というものが出てくる。
まずは以下の画像を見てみよう。
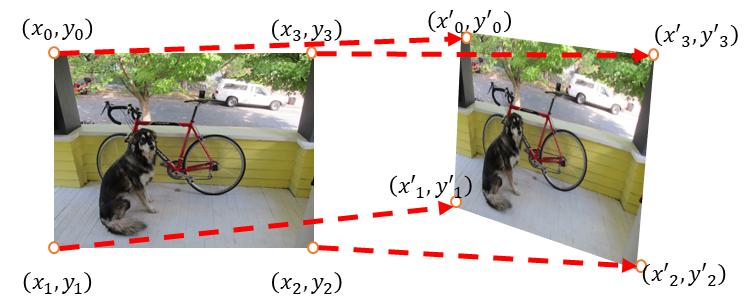
変換元の座標と、変換先の座標が該当する。
これにより、\(a~h\)の不明な変数8個。
自明な座標8点(定数としては16点)
これらにより8個の式を抱えた連立方程式が作成可能になる。
求めたい変数は8個だから8個の式で求まるはず。
元々9個のパラメータだったものを8個に減らしている。
その時の変形がここで生きてくる。
具体的な連立方程式は以下になる。
注意点としては、変数は\(x,y\)や\(x\prime,y\prime\)ではなく、\(a~h\)という点。
ここを読み間違えると、数式の意味がわからなくなる。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
ax_0+by_0+c-gx_0x_0\prime-hy_0x_0\prime=x_0\prime\\
dx_0+ey_0+f-gx_0y_0\prime-hy_0y_0\prime=y_0\prime\\
ax_1+by_1+c-gx_1x_1\prime-hy_1x_1\prime=x_1\prime\\
dx_1+ey_1+f-gx_1y_1\prime-hy_1y_1\prime=y_1\prime\\
ax_2+by_2+c-gx_2x_2\prime-hy_2x_2\prime=x_2\prime\\
dx_2+ey_2+f-gx_2y_2\prime-hy_2y_2\prime=y_2\prime\\
ax_3+by_3+c-gx_3x_3\prime-hy_3x_3\prime=x_3\prime\\
dx_3+ey_3+f-gx_3y_3\prime-hy_3y_3\prime=y_3\prime\\
\end{array}
\right.
\end{eqnarray}
\)
次のページへ
ここまでの方程式を行列で扱う話へ突入





コメント