元画像平面を3次元空間で表現
そして、話を射影変換に戻す。
元画像を3次元空間で表現しなおすのだが、
この画像のように解釈する。
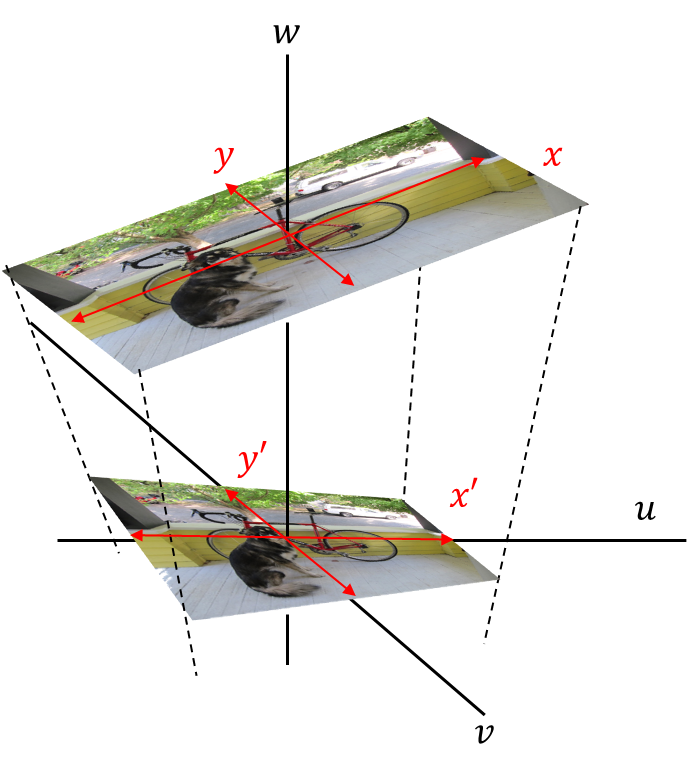
\((x,y)\)と\((u,v,w)\)は線形変換で求められる。
少なくとも2次関数とかにはならない。
よって、以下の変換式が成立するはず。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
u=ax+by+c \\
v=dx+ey+f\\
w=gx+hy+i
\end{array}
\right.
\end{eqnarray}
\)
感覚的にも正しいことはわかるだろう。
数学的に表現するならば、
「\(x,y\)を基底ベクトルとし、加えて、\(w\)方向の基本ベクトル。
この3つのベクトルの合成は全空間を表現できる。」
ってことになる。
(ここで基本ベクトルと、基底ベクトルの話が出てくる)
3次元空間を地面平面に落とし込む
ここでは3次元平面に浮かせた元画像平面を
地面平面に落とし込む場合の話をする。
地面平面の落とす、つまりこれが射影。
画像としてはこれを見るとわかるだろう。
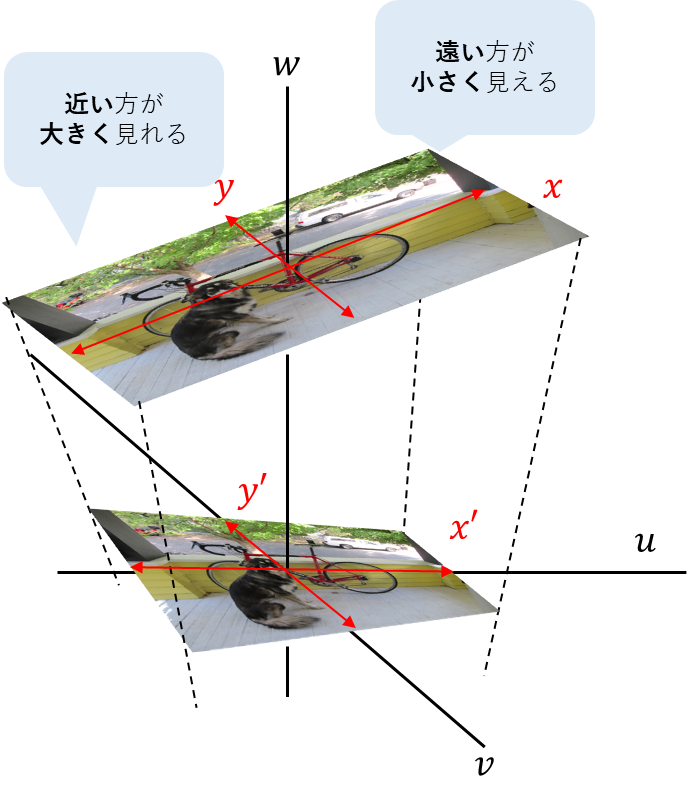
これを数式で表現する必要がある。
考え方はシンプル。
まず、\(x\prime\)と\(u\)、\(y\prime\)と\(v\)は間違いなく相関性は強い。
ここに対して高さ\(w\)の補正を掛ける。
つまり、「地面からの距離が離れるほど小さく見える」を数式で再現できればOK。
これらを加味した式は以下になる。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle x\prime=\frac{u}{w} \\
\displaystyle y\prime=\frac{v}{w}
\end{array}
\right.
\end{eqnarray}
\)
台形に利くのが\(w\)の部分。
これがアフィン変換にはない概念を生み出している。
\(w\)が無かったら、
移動、回転、伸縮くらいしかできそうもない。
一連の座標変換まとめ
これまでの一連の変換を再掲しよう。
元画像平面を3次元空間で表現
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
u=ax+by+c \\
v=dx+ey+f\\
w=gx+hy+i
\end{array}
\right.
\end{eqnarray}
\)
3次元空間を地面平面に落とし込む
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle x\prime=\frac{u}{w} \\
\displaystyle y\prime=\frac{v}{w}
\end{array}
\right.
\end{eqnarray}
\)
\(u,v,w\)を代入すると以下の式にできる。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle x\prime=\frac{ax+by+c}{gx+hy+i} \\
\displaystyle y\prime=\frac{dx+ey+f}{gx+hy+i}
\end{array}
\right.
\end{eqnarray}
\)
次のページへ
方程式を変形して見やすくし、行列形式の表現へ



コメント