MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第3章 その89【射影変換③】
MATLAB,Python,Scilab,Julia比較 第3章 その90【射影変換④】
MATLAB,Python,Scilab,Julia比較 第3章 その91【射影変換⑤】
MATLAB,Python,Scilab,Julia比較 第3章 その92【射影変換⑥】
MATLAB,Python,Scilab,Julia比較 第3章 その92【射影変換⑦】
を書き直したもの。
アフィン変換の拡張と言われている射影変換の話。
射影変換の理屈について語っていく。
射影変換の理屈
これから射影変換の理屈の部分を説明していくが、
そこそこのボリュームがある。
よって、2回に分けて説明。
説明の全体像は以下となる。
- 大まかな理屈
- 大まかな理屈を座標変換で説明
- 基本ベクトルと基底ベクトル
- 元画像平面を3次元空間で表現
- 3次元空間を地面平面に落とし込む
- 一連の座標変換まとめ
- 方程式の変形
- 行列表現
- アフィン変換との関係性
- 係数の求め方
- 係数の求め方(行列表現)
- 射影変換の処理の流れ
一個一個はそれほど難しくはないが、
数が多いのと因果関係が難しいから一個一個が簡単でもトータルだと簡単じゃなくなる面はある。
理屈の因果関係はシンプルで、上から順番に因果があると思えばOK。
大まかな理屈
まずは大まかな理屈。
これは画像で説明した方が早い。
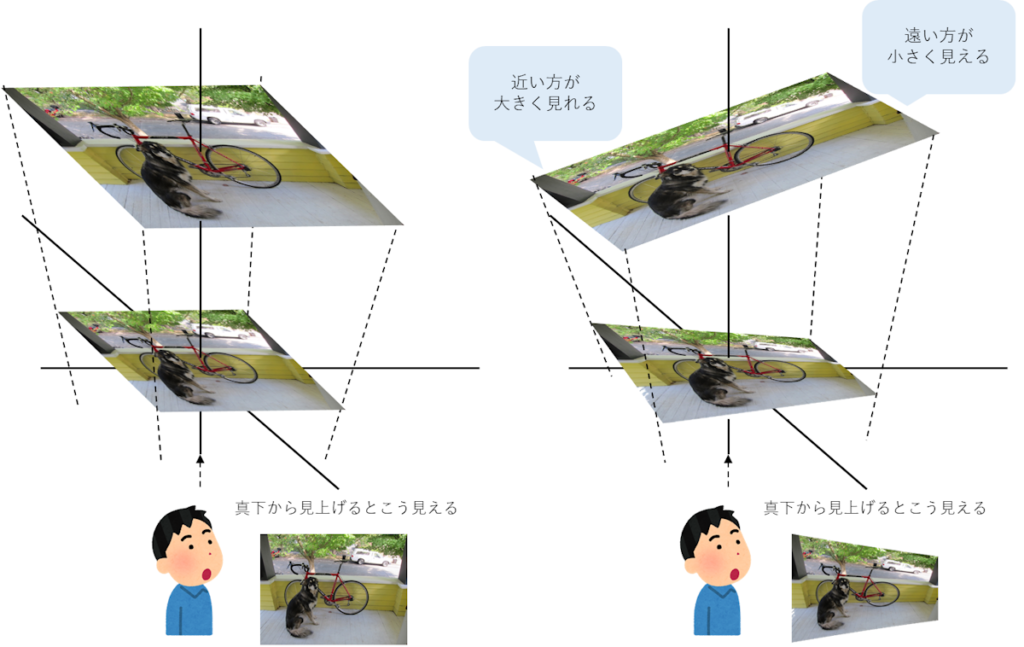
3次元空間で見た場合、近い方が大きく見えて、遠くの方が小さく見えるのは感覚的にもわかるだろう。
と言っても、ここからいきなり計算方法もわからない。
これを一つ一つひも解いていく。
大まかな理屈を座標変換で説明
先ほどの大まかな理屈を座標変換で表現すると以下のイメージになる。
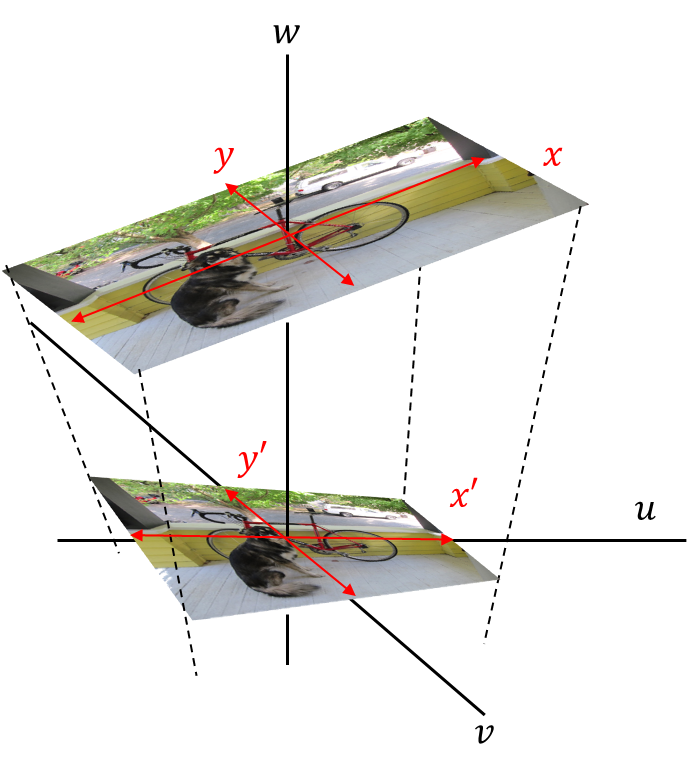
元画像の平面を\(x,y\)平面。
2種類の画像が存在数r空間を\(u,v,w\)空間。
射影が映り込む平明を\(x\prime,y\prime\)平面。
という感じになる。
よって、
\((x,y)\)→\((u,v,w)\)→\((x\prime,y\prime)\)
って流れで変換していく。
これでもまだ計算方法は見えてこないだろう。
基本ベクトルと基底ベクトル
直接的に射影変換には関連しないのだが、
基本ベクトルと基底ベクトルについて簡単に説明しておこう。
これはそれほど複雑な話ではない。
まずはこの図を見てみよう。
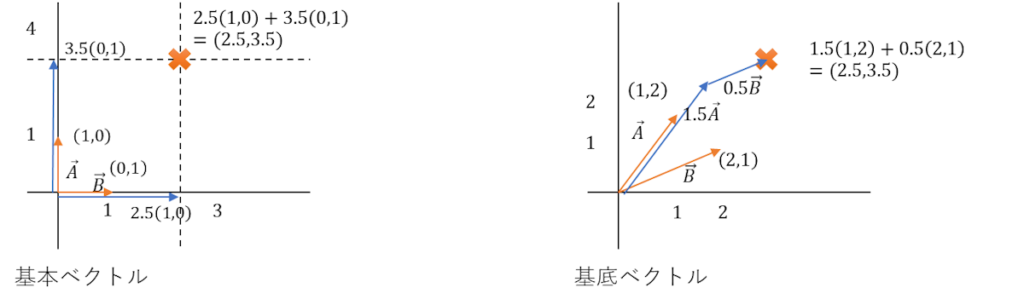
基本ベクトルの方は、平面上のベクトル表現の基本系というのはわかると思う。
基本ベクトルは、軸に沿った2本の単位ベクトル(大きさ1)になる。
これがあれば、すべての平面座標を表現できる。
基底ベクトルは
2本の交差するベクトル。
このベクトルも、すべての閉演座標を表現できる。
図の例では、(1,2)、(2,1)の2つのベクトルがあるが、
これを任意の倍率且つ合成すれば、あらゆる座標が表現可能だ。
基本ベクトルは、強烈な制約のついた基底ベクトルと言える。
次のページへ
元画像平面を3次元空間で表現するとどうなるか?





コメント