行列の結合法則の証明(行列サイズ一致の確認)
ここでは行列の結合法則の証明を行う。
以下の3つの行列があるとする。
A行列:\(l\times m\)行列
B行列:\(m\times n\)行列
C行列:\(n\times p\)行列
ABCの順序で行列の積は行えるが、任意のサイズの行列を示している。
まず、\((AB)C\)と\(A(BC)\)の行列のサイズが一致するか確認しておく。
\((AB)C\)の場合
\(
\begin{eqnarray}
&&\Big(l\times m) \times (m\times n) \Big)\times (n\times p)\\
&=&(l\times n)\times (n\times p)\\
&=&(l\times p)
\end{eqnarray}
\)
\(A(BC)\)の場合
\(
\begin{eqnarray}
&&(l\times m) \times \Big((m\times n) \times (n\times p)\Big)\\
&=&(l\times m) \times (m\times p)\\
&=&(l\times p)
\end{eqnarray}
\)
行列のサイズとしては一緒になる
行列の結合法則の証明(任意成分の証明)
次は任意の成分に着目した証明。
\(AB\)の任意成分(i,k)
\(
\displaystyle\sum_{j=1}^m a_{ij}b_{jk}
\)
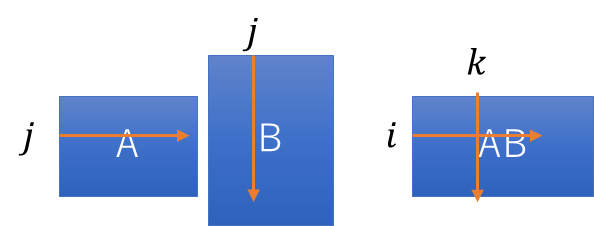
\((AB)C\)の任意成分(i,l)
\(
\begin{eqnarray}
&&\displaystyle\sum_{k=1}^n\bigg(\sum_{j=1}^m a_{ij}b_{jk}\bigg)c_{kl}\\
&=&\sum_{j=1}^m \sum_{k=1}^n a_{ij}b_{jk} c_{kl}
\end{eqnarray}
\)
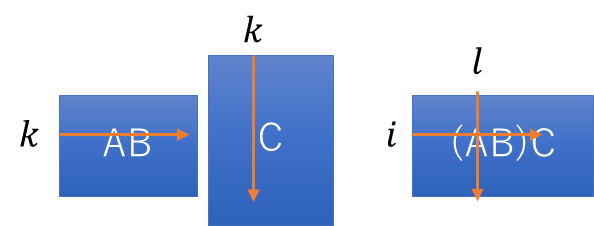
\(BC\)の任意成分(j,l)
\(
\displaystyle\sum_{j=1}^m b_{jk}c_{kl}
\)
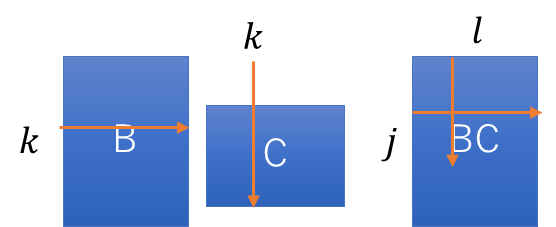
\(A(BC)\)の任意成分(i,l)
\(
\begin{eqnarray}
&&\displaystyle\sum_{j=1}^n a_{ij}\bigg(\sum_{k=1}^n b_{jk}c_{kl}\bigg)\\
&=&\sum_{j=1}^m \sum_{k=1}^n a_{ij}b_{jk} c_{kl}
\end{eqnarray}
\)
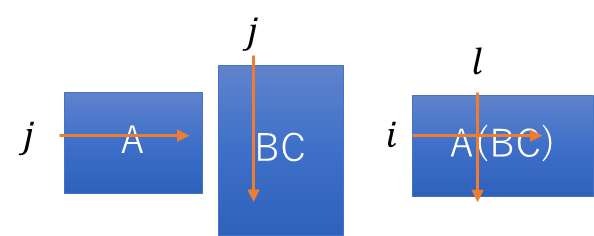
というわけで、行列の結合法則は成立する。
これにより、アフィン行列を事前に結合しても数学的には全く問題ないことが証明された。
が、まだこれだけでは解決できない問題が…。
まとめ
- アフィン行列の合成できる。
- 行列の結合法則について説明。
- 行列の結合法則を証明。
- 上記により、アフィン行列の合成が証明される。
MATLAB、Python、Scilab、Julia比較ページはこちら




コメント