MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その46【二乗和誤差①】
MATLAB,Python,Scilab,Julia比較 第2章 その47【二乗和誤差②】
を書き直したもの。
正規方程式を導出するまでの説明。
二乗和誤差とそれを多変量対応にするためのに一般化ついて説明とその証明を行う。
ロードマップ【再掲】
今回は、二乗和誤差の話になる。
ロードマップで、位置づけを確認しておこう。

二乗和誤差
二乗和誤差については以前、最小二乗法の誤差関数として取り扱ったことはある。
正しいを思われる線との誤差を2乗にしたものを誤差関数として、この誤差関数を可能な限り小さくしたものが求めたい線。
という理屈であり、今回も理屈のレベルでは同一。
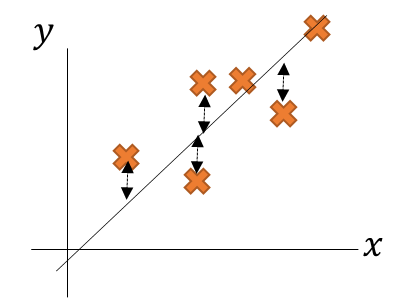
その時に導出した、一次関数の時の誤差関数こと二乗和誤差を再掲しておこう。
\(
\begin{eqnarray}
L(a,b)&=&\displaystyle\sum_{i=0}^n\{y_i -(ax_i +b)\}^2 \\
&=&\displaystyle a^2\sum x_i^2+nb^2+\sum y_i^2-2a\sum x_i y_i -2b\sum y_i +2ab\sum x_i
\end{eqnarray}
\)
最小二乗法との差異
理屈のレベルでは同一と言ったが、何もしなくてOKというわけではない。
多変量を扱えるよう、より一般化したものを導出する必要がある。
一般化というと簡単になるようなイメージで聞こえるかもしれないが、
数学の世界における一般化は、抽象度を引き上げて適用できる範囲を広げるって意味になるから、大体難しい方になる。
以前の最小二乗法の時の誤差関数は、1変量1次関数を想定したものだった。
これを多変量にするのが、今回に於ける一般化になる。
多変量って?
多変量は、言い換えると多変数。
簡単に言うと、入力が複数になったってだけ。
複数になったことで多変量。
多変量だからベクトルで表現できる。
って寸法。
ベクトルがあるからこそ楽に扱える。
二乗和誤差を多変量で表現
二乗和誤差を多変量で表現すると以下になる。
関数\(f\)が求めたい線で、\(y_i\)が実際に観測できた値。
\(
L(x_1,\dots,x_m)=\displaystyle\sum_{i=1}^n\{f(x_{1i},\dots,x_{mi})-y_i\}^2
\)
次に、左辺をベクトル、行列で表現する。
これが一般化。
少しややこしいが、
\(A\)が入力変数(または説明変数)をまとめた行列
\(\vec{x}\)が各係数をまとめたベクトル
\(b\)が出力変数(または目的変数)をまとめたベクトル
注意点としては、ベクトルの二乗をしている部分は厳密には内積と同じになる。
\(
L(x_1,\dots,x_n)=(A\vec{x}-\vec{b})^2
\)
ベクトル、行列を具体的にすると?
ベクトル、行列の表現がよくわからないかもしれない。
この場合、逆に具体化させると良い。
以前までやったた一次関数を扱う場合、\(A,\vec{x},\vec{b}\)は以下になる。
\(
A=
\begin{bmatrix}
x_1 & 1\\
x_2 & 1\\
\vdots & \vdots\\
x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)
じっくり読んで、式を展開するとわかるが、
表現が変わっただけで、普通の最小二乗法の誤差関数と同じ形になるはずだ。
扱う方程式の項数が増えれば、
それに合わせて行列\(A\)の列と
ベクトル\(\vec{x}\)の要素が増える。
項数が増えることは変数が増えるってことだから、
これで多変量ってのに対応できたことになる。
ここまで来たら、今までの知識を統合してあとは正規方程式を求めるのみ。
まとめ
- 二乗和誤差に関しては、以前の最小二乗法の誤差関数で扱ってはいる。
- 「正しいを思われる線との誤差を2乗にしたもの」という意味自体は変わらない。
- 二乗和誤差を多変量で表現。
- ベクトル、行列で表現する。
- 一般化した後に具体化して確認。
MATLAB、Python、Scilab、Julia比較ページはこちら






コメント