バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、今後の方針として以下を出した。
- フーリエ変換後の逆フーリエ変換をして元波形に戻るか。
- 抽出したい周波数範囲を特定。
- 極大値、極小値のタイミングとその時の単価特定。
今回はMATLAB版フーリエ変換、逆フーリエ変換を個別株チャートに対して実施してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
MATLAB版フーリエ変換、逆フーリエ変換を個別株チャートに対して実施

じゃ、とりあえず、個別株に対してMATLAB版フーリエ変換、逆フーリエ変換やっちゃうよー。

たぶん問題無いはず。

まぁ簡単な波形では動いたけど、複雑波形の場合どうなるかってのは不安だよね。

(なぜ発言がこうも他人事になってるのか・・・。)
結果の波形

結果はこんなん。
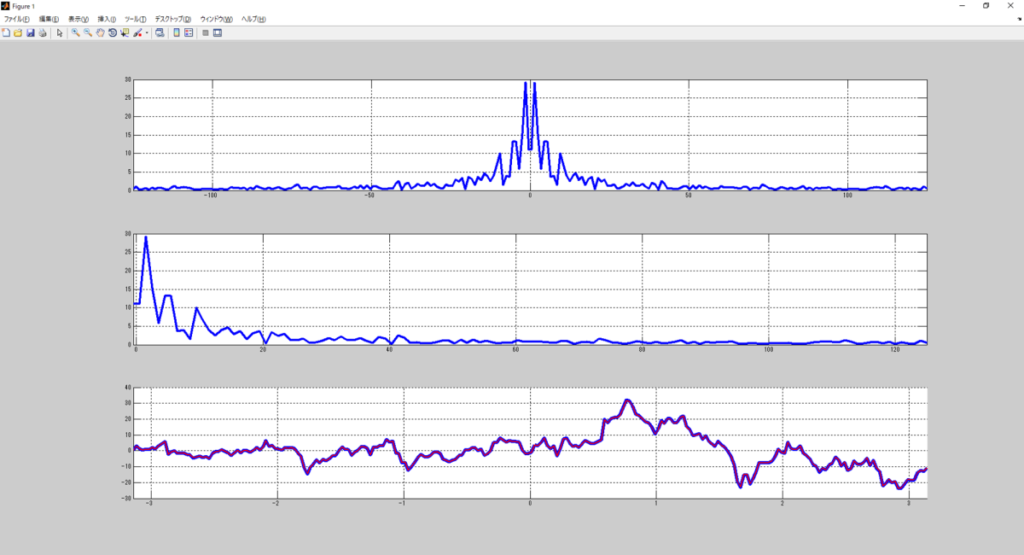

これは最大周波数を125[Hz]にしているので、
DFTやFFTでやったのと同じ結果ではあるな。
結果の波形(最大周波数20[Hz]版)

じゃー、最大周波数を20[Hz]にしてみよう。
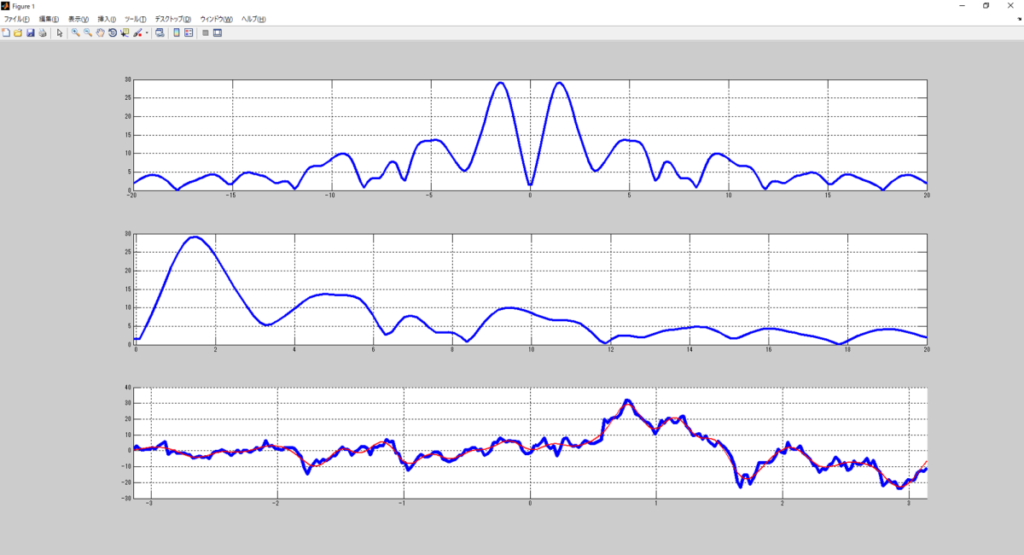

波形が元に戻り切らなくなっちゃったね・・・。

高周波が軒並みカットされたからね。
でも、元に戻ることが保証された構成なので、
0~20[Hz]の周波数特性にだけ着目すれば良いと思うよ。

そっか。
意図的に最大周波数を押さえてるわけだから、
こうなること自体は当たり前なのか。
高周波を入れれば元に戻ることはさっき証明したから気にしなくても良い。
って理屈か。
取り出す周波数帯は?

で、ここから取り出す周波数帯を決めるわけだけど、
FFTの時は10[Hz]を中心として9[Hz]~11[Hz]を取り出したんだよね。
そういう意味では今回も似たような性質なのかな?
若干10[Hz]より低周波より重みが寄ってそうだけど。

この感じだと、目算で
8.4[Hz]~11.8[Hz]の取り出しで良いんじゃないかな?

そっか。
周波数分布の分解能が細かくなってるから、そういう取り出し方ができるのか。

実際に取り出した場合のことはPython側でも同じことができるのを確認した後にやってみよう。
まとめ

まとめだよ。
- MATLAB版フーリエ変換、逆フーリエ変換を個別株チャートに対して実施。
- DFT、FFTと同等の分解能で実施。
- 逆フーリエ変換で元波形に戻った。
- 最大周波数を落として分解能を上げてみた。
- 逆フーリエ変換で元波形には戻らない。
- 高周波分を捨てているため発生。
- 元に戻ることは先の処理で証明しているので問題無し。
- DFT、FFTと同等の分解能で実施。
バックナンバーはこちら。




コメント