バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、収支シミュレーション向けた作業として以下を実施。
- 終値から平均値を引いた値と算出したものをcsvにしていたが、終値をそのままcsv化。
- MATLAB、Pythonで終値を取り込んでから平均値を引く方式に変更。
今回は、IFFTから出力された波形の極大値、極小値の求め方について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
極値の求め方

今回は、極大値と極小値の求め方か・・・。

以前もいったが、それほど難しい話では無い。

まぁそこを解説してもらおうか。

端的に言うと、微分して0になれば極値だ。
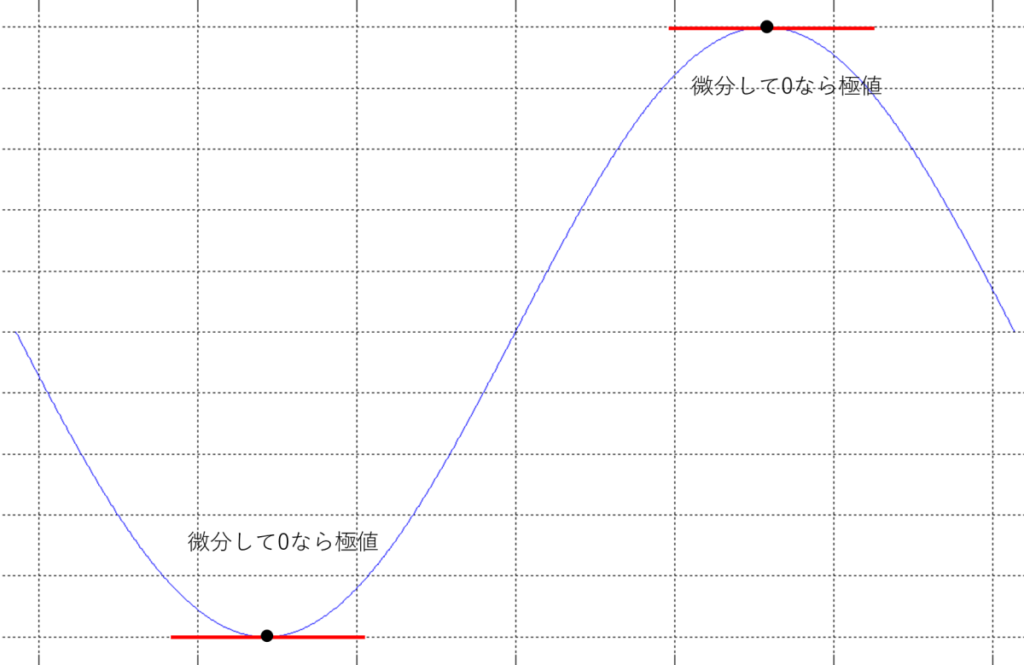

まぁ、なるほどとは思ったけど、
「極値が分かる」ってのは分かったけど、
これが極小値なのか極大値なのかがわからないような・・・。
極大値と極小値の求め方

極大値は、「微分値がプラス→0→マイナス」となるところ。
極小値は、「微分値がマイナス→0→プラス」となるところ。

???

絵で書くとこんな感じだよ。
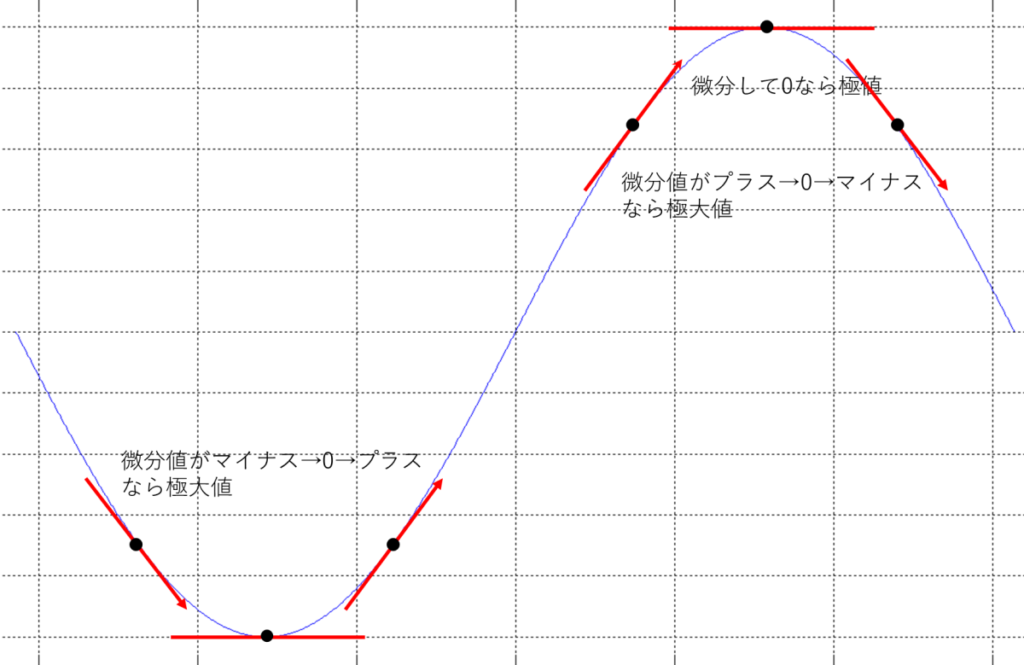

ほう。
確かに言われてみるとそうだね。
微分して0でも極値じゃない場合も

ちなみに微分して0になったとしても極値ではないパターンもある。

そんなパターンあるの?
思いつかないけど?

こんなパターンだな。
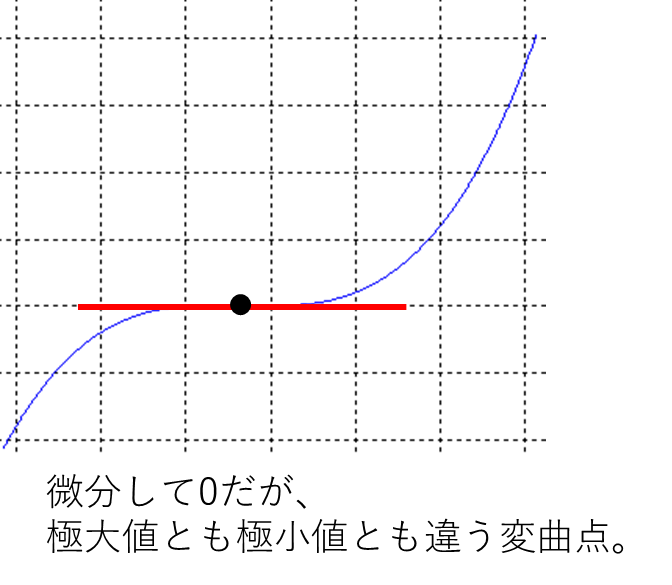

確かにこれは極値とは言えないね。

ちなみにこのグラフの式は以下になるね。
\(y=x^3+x^2\)
↓微分して\(x=0\)時の傾きを算出
\(y\prime=3x^2+2x\)
\(y\prime=3(0)^2+2(0)=0\)

ちなみに、以下でもいいんだけど、「変曲点の傾き0」の見やすさ重視で上の式を使った。
\(y=x^3\)
↓微分して\(x=0\)時の傾きを算出
\(y\prime=3x^2\)
\(y\prime=3(0)^2=0\)

こんなシンプルな関数でも発生し得るのか・・・。
微分するには?

どっちにしても微分をする必要があると思うのだけど、
プログラム的にはどうするの?

引き算するだけだな。

引き算だけだと微分にならなくない?
たしか、dtの兼ね合いも考える必要があったような・・・。

今回欲しいのは厳密な微分値でも近似な微分値でも無くて、
微分した結果がプラスか、マイナスかだけなので、
引き算でOKなんだよ。

あ、そっか。
確かに接線傾きの正負を知りたいだけだから、それだけでいいのか。

さらに、微分じゃなくて差分であるが故に微分値0を捕まえることはほぼ不可能。
よって、
極大値を探す場合は差分の結果マイナス。
極小値を探す場合は差分の結果プラス。
の点を探すことになる。

確かに離散的なデータなわけだから理想的な微分ができるわけじゃないもんね。

というわけで、次回は今回の話を元に具体的なプログラムにするとどうなるか?
ってところだな。

(今回は珍しくわかりやすかった)
まとめ

まとめだよ。
- 微分して0になれば極値。
- 極大値は、「微分値がプラス→0→マイナス」となるところ。
- 極小値は、「微分値がマイナス→0→プラス」となるところ。
- 「微分して0」でも極値にならないパターンもある。
- 3次関数とかが代表的。
バックナンバーはこちら。




コメント