バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回までで、MATLABとPythonの論理インデックス検索と線形インデックス検索について確認。
そうほう似たような形で実施可能ではあるが、
行列の場合は若干異なる。
今回はベクトルに対して実施するため、恐らくオリジン以外の大きな差異は出ない。
そして、今回はPython(Numpy)側のバンドパスフィルタを実施する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
Python(Numpy)によるバンドパスフィルタ

太郎くん
論理インデックスの話が出て途中になっちゃったけど、
バンドパスフィルタのPython(Numpy)側が残ってるね。

フクさん
そうそう。
よって、今回はPython(Numpy)版のバンドパスフィルタを試してみる。

太郎くん
特に大きな差ってのは無いのかな?

フクさん
基本的な流れは全く一緒だ。
余裕があればMATLABコードと比較して見ると良いだろう。
実際のコード

フクさん
そして実際のコードがこれになる。
import numpy as np
import matplotlib.pyplot as plt
N=1024
L=np.pi
x=np.linspace(-L,L,N)
k=np.arange(-N/2,N/2)
ft=np.sin(x)+np.sin(3*x)+np.sin(7*x)
fig = plt.figure()
# 変換前波形
ax1 = fig.add_subplot(4, 1, 1)
ax1.plot(x,ft)
ax1.set_title('f(t)')
# FFT後にローテーション
Fw=np.fft.fft(ft)
Fw_tmp = np.roll(Fw,int(N/2))
ax2 = fig.add_subplot(4, 1, 2)
mask = (-10<=k) & (k<=10)
ax2.plot(k[mask],np.abs(Fw_tmp[mask]))
ax2.set_title(r'$F(\omega)$')
# 特定周波数のみ抽出
Fw_Filter=Fw_tmp;
Hz = 3;
Low = Hz-0.1;
High = Hz+0.1;
Fw_Filter[ ( k< -High) | ((-Low < k) & (k <= 0)) | ((0 <= k) & (k < Low)) | (High < k)]=0;
ax3 = fig.add_subplot(4, 1, 3)
ax3.plot(k[mask],np.abs(Fw_Filter[mask]))
ax3.set_title(r'$F(\omega)$ expansion')
# IFFT前にローテーション
fx=np.fft.ifft(np.roll(Fw_Filter,int(N/2)))
ax4 = fig.add_subplot(4, 1, 4)
ax4.plot(x,fx.real)
ax4.set_title('f(x)')
plt.show()実行結果

フクさん
そして結果がこれ。
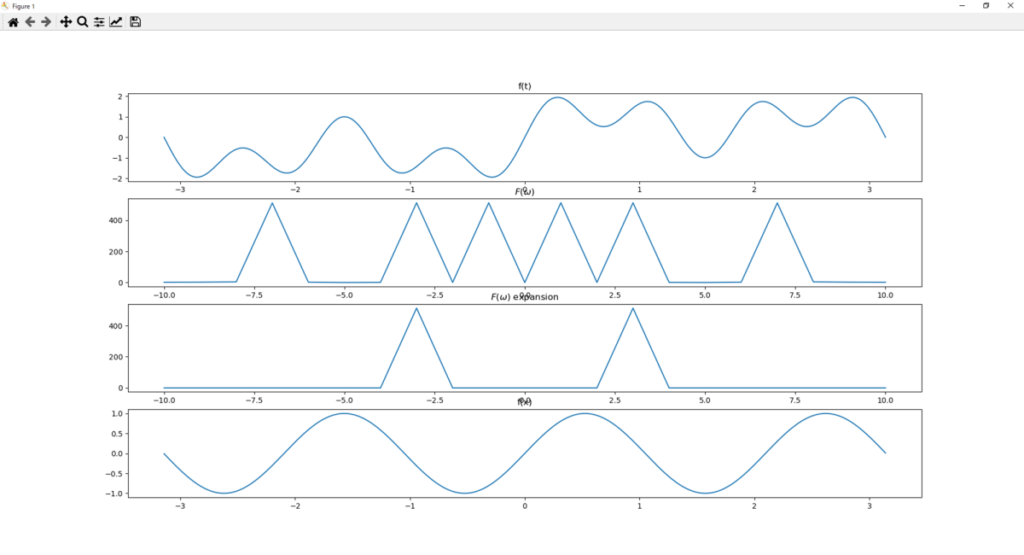

太郎くん
MATLABの時と同じ結果になった。
Pythonでも問題無いってことだね。

フクさん
まぁ同じことさせてるしね。
ダメだったらコード側がおかしいってことになるな。
まとめ

フクさん
まとめだよ。
- Python(Numpy)によるバンドパスフィルタのコード作成。
- 上記コードを実行して見た。
- MTALABと同じ結果が得られることを確認。
- よって、MATLAB、Python双方でFFT、IFFTによる特性周波数の抽出が可能と言える。
バックナンバーはこちら。




コメント