バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、MATLABで複数の周波数のsin波を合成したもの大してFFT&IFFT実施してみた。
想定通りの周波数分布になることが確認できた。
今回はこれのPython版を作成する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
複数の周波数のsin波を合成したもの大してFFT&IFFT(Python版)

フクさん
じゃ、さっそく前回のMATLABコードのPython版を貼っておこう。
import numpy as np
import matplotlib.pyplot as plt
N=1024
L=np.pi
x=np.linspace(-L,L,N)
k=np.arange(0,N)
ft=np.sin(x)+np.sin(3*x)+np.sin(7*x)
fig = plt.figure()
ax1 = fig.add_subplot(4, 1, 1)
ax1.plot(x,ft)
ax1.set_title('f(t)')
Fw=np.fft.fft(ft)
ax2 = fig.add_subplot(4, 1, 2)
ax2.plot(k,np.abs(Fw))
ax2.set_title(r'$F(\omega)$')
ax3 = fig.add_subplot(4, 1, 3)
ax3.plot(k[0:10],abs(Fw[0:10]))
ax3.set_title(r'$F(\omega)$ expansion')
fx=np.fft.ifft(Fw)
ax4 = fig.add_subplot(4, 1, 4)
ax4.plot(x,fx.real)
ax4.set_title('f(x)')
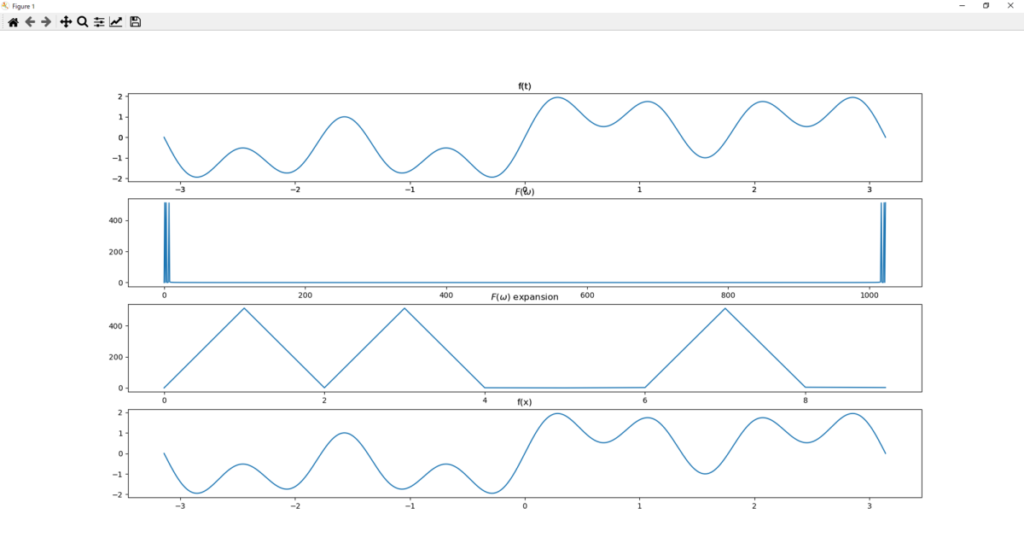
plt.show()動作結果

フクさん
そして結果。
まぁ当然ではあるが、MATLABの時と一緒だな。
入力サンプリング期間を伸ばした版

太郎くん
これも同じく入力サンプリング期間を延ばしてみよう。
L=np.pi
↓
L=2*np.pi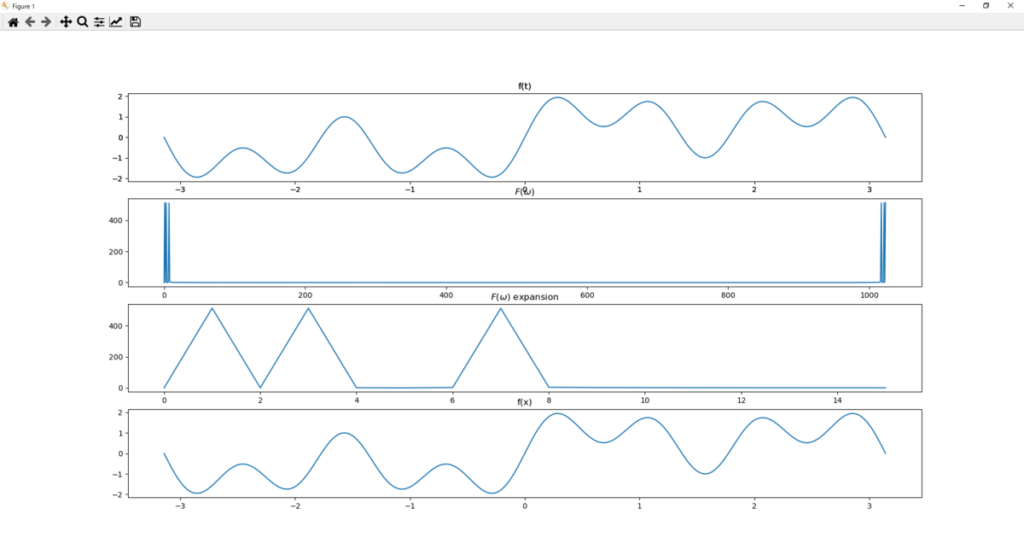

太郎くん
うん。
こっちもOKそうだ。

フクさん
大体FFTには慣れてきたんじゃない?

太郎くん
そうだね。
理屈の方はイマイチだけど、
出力が何を示しているのかは大体理解出来てきたよー。

フクさん
ならば、そろそろ次のステージに行くとするか。

太郎くん
(なんか、ヤバイ雰囲気が・・・。)
まとめ

フクさん
まとめだよ。
- 複数の周波数のsin波を合成したもの大してFFT&IFFT実施のPython版。
- 当然ではあるが、同一の結果が得られた。
- 加えて、入力サンプリング期間を延ばしたものも実施。
- これも当然、同一の結果が得られた。
- FFT,IFFTの理屈は兎も角として使い方に関してはなんとなく慣れてきたところ。
バックナンバーはこちら。




コメント