バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、これまでMATLABでやったのをPythonでやり直した。って話。
MATLAB、Python(Numpy)のFFT,IFFTは同一の数式を使用しているので、互換性はあると思って良い。
今回もFFT,IFFT実験だが少し複雑め波形で行う予定。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
波形の合成

次はもう少し複雑な波形をFFTに掛けて見る。

具体的にはどんな波形?

異なる周波数のsin波の合成だな。

sin波の合成・・・ってどうやるんだ?

単純に足し算をすればOKだよ。
こんな感じ。
\(f(t)=sin(t)+sin(3t)+sin(7t)\)

あ、それだけか。
ならチョロい。
MATLABコード

そして、今回の実験コードがこれだ。
まぁ変換元関数を先ほどのsin波の合成関数に置き換えただけだけど。
N=1024;
L=pi;
x=linspace(-L,L,N);
k=0:N-1;
ft=sin(x)+sin(3*x)+sin(7*x);
subplot(4,1,1);
plot(x,ft);
title('f(t)');
Fw=fft(ft);
subplot(4,1,2);
plot(k,abs(Fw));
title('F(\omega)');
subplot(4,1,3);
plot(k(1:10),abs(Fw(1:10)));
title('F(\omega) expansion');
fx=ifft(Fw);
subplot(4,1,4);
plot(x,fx);
title('f(x)');動作結果

そして動作結果がこれ。
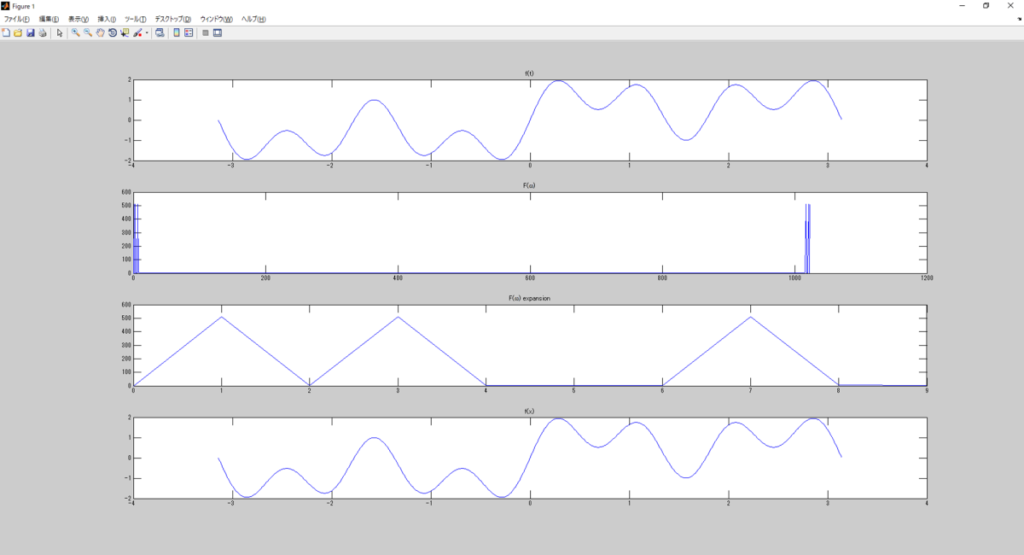

1[Hz]、3[Hz]、7[Hz]が抽出できてて、
ちゃんとIFFTで元の波形に戻ってるね。

なるほど。
確かに多少複雑な波形でも自明な物であれば、検証できるってことなのか。

そうそう。
入力サンプリング期間を延ばす

これも、入力サンプリング期間を延ばすと、周波数分布は変わるのかな?

変わるはずだ。
以下の変更を入れて動作した結果を見てみよう。
L=pi;
↓
L=2*pi;
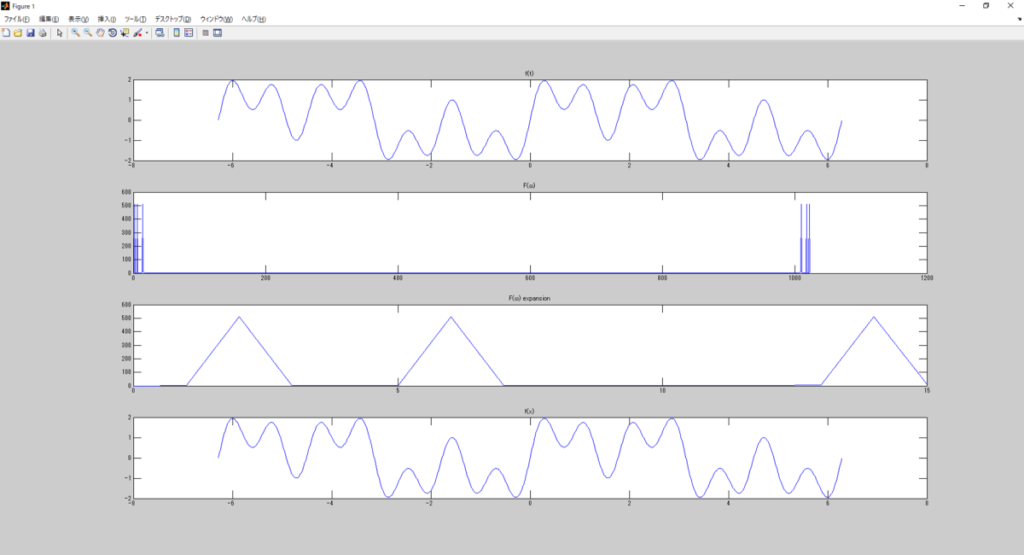

あ、ホントだ。

じゃーこれのPython版もやっておかないとね。
まとめ

まとめだよ。
- 複数の周波数のsin波を合成したもの対してFFT&IFFT実施。
- 波形の合成は単純に足し算するだけ。
- 想定通りの周波数分布になった。
- 試しに入力サンプリング期間を2倍に伸ばしてみた
- 想定通り、周波数が2倍になる分布に変化。
バックナンバーはこちら。




コメント