【入門】状態空間モデル超基礎【数値計算】

シンプルな微分方程式
状態量の定義
運動方程式を紐解いていく
各種方程式を見て
状態方程式の組み上げ
出力方程式の組み上げ
各種行列と外部設定変数
まとめ

シンプルな微分方程式

シンプルな微分方程式の代表格である、
ニュートンの運動方程式を状態空間モデルで表現してみる。

ニュートンの運動方程式
\(\vec{F}=m\vec{a}\)

そして、以下の問いを解くものとする。

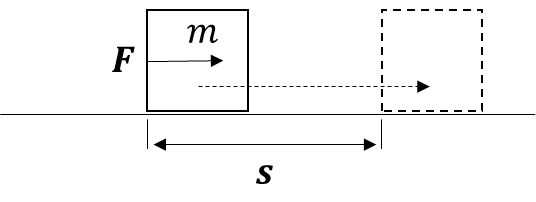
質量\(m\)の物体を、力\(\boldsymbol F\)を加え続けて距離\(\boldsymbol s\)分移動させた。
距離\(\boldsymbol s\)を出力(観測)とした状態空間モデルを作成せよ。
尚、運動方程式は以下とし、摩擦や重力は無視する。

\(m \ddot{s}(t)=\boldsymbol F(t)\)

状態量の定義

入力と出力は決まっているので、
状態量\(\boldsymbol x\)を定義する必要がある。

運動方程式の変数は以下。

力\(\boldsymbol F\)
距離\(\boldsymbol s\)
速度\(\boldsymbol v\)
加速度\(\boldsymbol a\)
質量\(m\)

尚、質量\(m\)は今回は変数ではなく係数という位置づけとする。

加速度\(\boldsymbol a\)との相関性が強い力\(\boldsymbol F\)から距離\(\boldsymbol s\)を求めるため、
状態量としては、距離\(\boldsymbol s\)、速度\(\boldsymbol v\)とする。

状態量
\(
\boldsymbol x=
\begin{bmatrix}
v(t) \\
s(t)
\end{bmatrix}
\)

これに伴って状態方程式の解である、\(\dot{\boldsymbol x}\)は
状態量の一階微分のため、以下になる。

状態方程式の解
\(
\dot{\boldsymbol x}=
\begin{bmatrix}
\dot{v}(t) \\
\dot{s}(t)
\end{bmatrix}
\)

運動方程式を紐解いていく

ここから運動方程式を紐解いていく。

運動方程式
\(m \ddot{s}(t)=\boldsymbol F(t)\)

距離\(s(t)\)、速度\(v(t)\)、加速度\(a(t)\)の関係
\(\ddot{s}(t)=\dot{v}(t)=a(t)\)
\(\dot{s}(t)=v(t)\)

上記より
\(
\begin{eqnarray}
m \dot{v}(t) &=& F(t) \\
\dot{v}(t) &=& \displaystyle \frac{F(t)}{m}\dots(1) \\
\dot{s}(t) &=& v(t)\dots(2)
\end{eqnarray}
\)

各種方程式を見て

微分は出てくるけど、そこは距離、速度、加速度の関係性で吸収される。
よって、微分そのものはあまり気にしなくて良い。
あとは普通に移項して、\(\dot{\boldsymbol x}\)の中身である、
\(\dot{v}(t)\)と\(\dot{s}(t)\)が求められる方程式が出てくる。

状態方程式の組み上げ

状態方程式
\(\dot{\boldsymbol x}=A\boldsymbol{x}+B\boldsymbol{u}\)

これに対して今回導出した方程式である(1)(2)を適用すると以下になる。

\(
\begin{bmatrix}
\dot{v}(t) \\
\dot{s}(t)
\end{bmatrix}=
\begin{bmatrix}
0 && 0 \\
1 && 0
\end{bmatrix}
\begin{bmatrix}
v(t) \\
s(t)
\end{bmatrix}+
\begin{bmatrix}
1/m \\
0
\end{bmatrix}
F(t)
\)

これは行列演算の表現になっただけで、
(1)(2)の方程式と全く同じ意味の数式になる。

出力方程式の組み上げ

出力方程式
\(\boldsymbol y=C\boldsymbol{x}+D\boldsymbol{u}\)

これに対して、出力させたい変数は距離\(s(t)\)
そうなると以下になる。

\(
\boldsymbol{y}=
\begin{bmatrix}
0 && 0 \\
0 && 1
\end{bmatrix}
\begin{bmatrix}
v(t) \\
s(t)
\end{bmatrix}+
\begin{bmatrix}
0 \\
0
\end{bmatrix}
F(t)
\)

しかし、ここでは内部パラメータを全部参照しておきたいので、
以下にしておく。

\(
\boldsymbol{y}=
\begin{bmatrix}
1 && 0 \\
0 && 1
\end{bmatrix}
\begin{bmatrix}
v(t) \\
s(t)
\end{bmatrix}+
\begin{bmatrix}
0 \\
0
\end{bmatrix}
F(t)
\)

つまり、出力行列\(C\)次第で出力される状態量が確定する。
念のためすべての状態量を参照できるようにすることは多い。

これで運動方程式を元にした超シンプルな状態空間モデルは完成となる。