【入門】状態空間モデルをPID制御【数値計算】

PID制御の離散化
ブロック線図
PID制御器を加味した構成図
1/60の根拠
各種コードへ
まとめ

PID制御の離散化

微分解法はオイラー法。
注意点は[Nsec]という単位時間を最終的には $T_{1}$ に置き換えて単位時間も調整可能にしている点

$u (t) = \int {K_{p} \dot{e} (t) + K_{i} e (t) d t + K_{d} \ddot{e} (t)} \dots (変形式)$
$\dot{e} (t)$ と $\ddot{e} (t)$ をオイラー法で解決する。

$\begin{aligned} \dot{e} (t) & = & \frac{e (t) - e (t - Δ T)}{Δ T [N s e c]} \\ = & \frac{e (t) - e (t - Δ T)}{Δ T / T_{1}} \\ = & \frac{{e (t) - e (t - Δ T)} T_{1}}{Δ T} \end{aligned}$

上記の $e (t)$ に $\dot{e} (t)$ を代入することで2階微分となるため、
$\begin{aligned} \ddot{e} (t) & = & \frac{{\dot{e} (t) - \dot{e} (t - Δ T)} T_{1}}{Δ T} \\ = & \frac{\frac{{e (t) - e (t - Δ T)} T_{1}}{Δ T} - \frac{{e (t - Δ T) - e (t - Δ T - Δ T)} T_{1}}{Δ T}}{Δ T} \\ = & \frac{T_{1}}{Δ T} {\frac{T_{1}}{Δ T} {e (t) - e (t - Δ T)} - \frac{T_{1}}{Δ T} {e (t - Δ T) - e (t - 2 Δ T)}} \end{aligned}$

積分に関しては以下で近似

$\int x (t) d t = \sum x (t - Δ T) + x (t) \frac{Δ T}{T_{1}}$

それぞれをPID制御の変形式に代入する

$\begin{aligned} u (t) & = & \int {K_{p} \dot{e} (t) + K_{i} e (t) d t + K_{d} \ddot{e} (t)} d t \\ = & \int {{K_{p} \frac{T_{1}}{Δ T} {e (t) - e (t - Δ T)} + K_{i} e (t) \\ + & K_{d} \frac{T_{1}}{Δ T} {{\frac{T_{1}}{Δ T} {e (t) - e (t - Δ T)} \\ - & \frac{T_{1}}{Δ T} {e (t - Δ T) - e (t - 2 Δ T)}}} d t \end{aligned}$

最後の式の色分けしたところは同一(実際には1周期過去)と見なせる。
これによりブロック線図にした際はそれほど複雑にはならない。

ブロック線図

上記数式に合わせて起こしたブロック線図が以下となる。

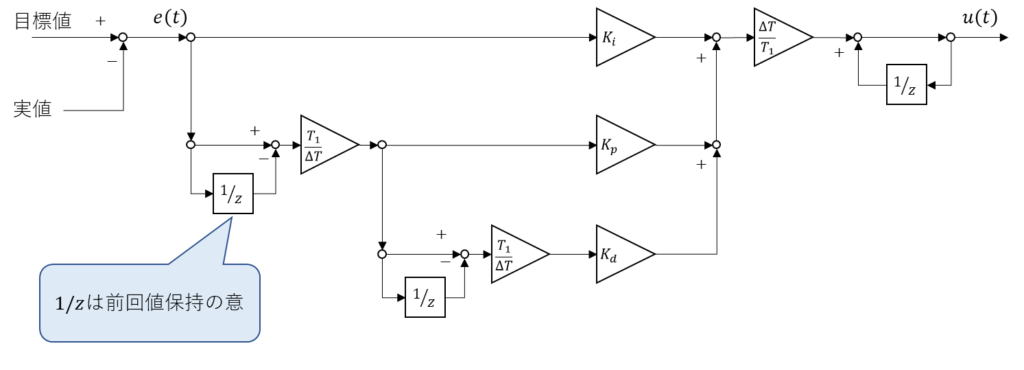
同じ数式のところはブロック線図としては同一の信号線を参照すれば良いからいい感じに最適化される。

PID制御器を加味した構成図

PID制御器を加味した構成図が以下となる。
ちなみに、PID制御器内部はおおよそ-1～1の範囲で値が動くよう
フィードバック側は1/60にしている。

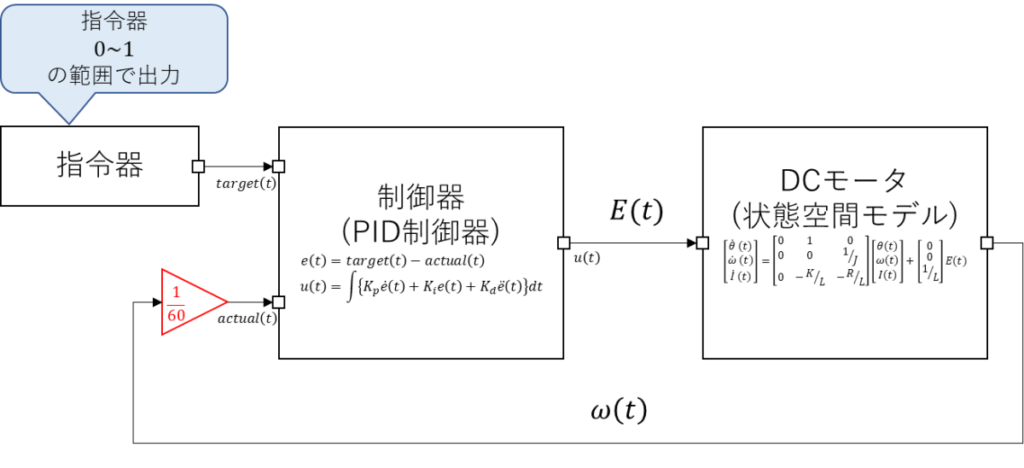
1/60の根拠

$E (t) = 1$ とした際に、角速度 $ω (t)$ はおおよそ $60 [r a d / s e c]$ に収束していた。
PID制御器の内部信号の動作範囲を-1～1としたい場合は1/60するとちょうど良い感じになる。
いわゆる正規化で、こうすることでPID制御器は割と純粋な数学の世界で動作し、
挙動が読みやすくなる。