【入門】状態空間モデルをPID制御【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
状態空間モデルを制御したい
大まかな流れ
いままでの状態空間モデルの制御を構成図として書くと。
今回の構成
PID制御の基本式
PID制御の変形の動機
PID制御の変形式
次のページへ

はじめに

の、
MATLAB,Python,Scilab,Julia比較その72【PID制御①】
MATLAB,Python,Scilab,Julia比較その73【PID制御②】
MATLAB,Python,Scilab,Julia比較その74【PID制御③】
MATLAB,Python,Scilab,Julia比較その75【PID制御④】
MATLAB,Python,Scilab,Julia比較その76【PID制御⑤】

を書き直したもの。

DCモータ状態空間モデルにPID制御器を用いて制御しようという話。
その前にPID制御器の離散化、ブロック線図の作成が必要。
ここまでやればコードに落とし込むのは難しくない。

状態空間モデルを制御したい

前回まででDCモータの状態空間モデルは作成したが、
実際は制御器から制御される構成になることが多い。
よって、PID制御器をプログラムで表現可能な状態まで持って行くのが本記事の目的となる。

大まかな流れ

以下の手順でPID制御器のコード化手前まで持っていく。

前回までの構成の確認
今回の構成を確認
PID制御器の基本式の確認
PID制御器の基本式変形
PID制御器の離散化
離散化PID制御器のブロック図
PID制御器を加味した構成図

一つ一つは大した話では無い。
「PID制御器の離散化」あたりが若干鬼門だが、
微分解法はオイラー法にするため、それほど難しいことにはならない。(はず)

いままでの状態空間モデルの制御を構成図として書くと。

前回までの状態空間モデルの構成はいわゆるオープンループ制御の構成となる。

前回までの状態空間モデルの構成

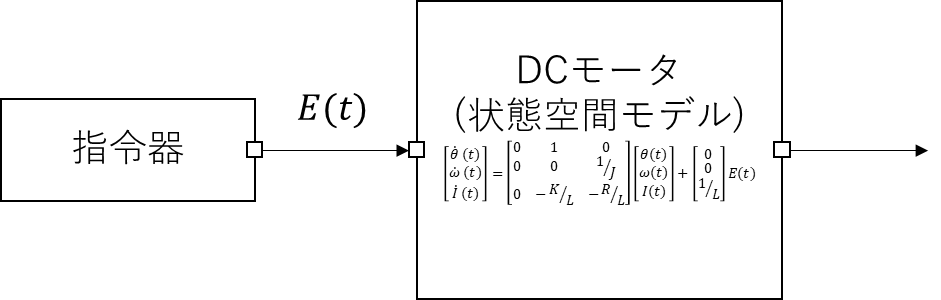
開ループ制御（かいループせいぎょ）またはオープンループ制御（英: Open-loop control）は、制御理論において、現在の状態と制御システムのモデルのみを使って入力に対して計算を行う制御を指す。フィードバックを使わずに、入力が所定の目標値に達したかを判断することを特徴とする。つまり、開ループ制御システムは制御しているプロセスの出力を観測しない。したがって、真の開ループシステムは機械学習には採用されず、発生させた誤りを訂正することもできない。また、システムにおける外乱を補償することもできない。
Wikipediaより(https://ja.wikipedia.org/wiki/%E9%96%8B%E3%83%AB%E3%83%BC%E3%83%97%E5%88%B6%E5%BE%A1)

今回の構成

今回のPID制御器を追加した場合は以下のような構成になり、
いわゆるクローズループ制御となる。

今回の状態空間モデルを制御する構成

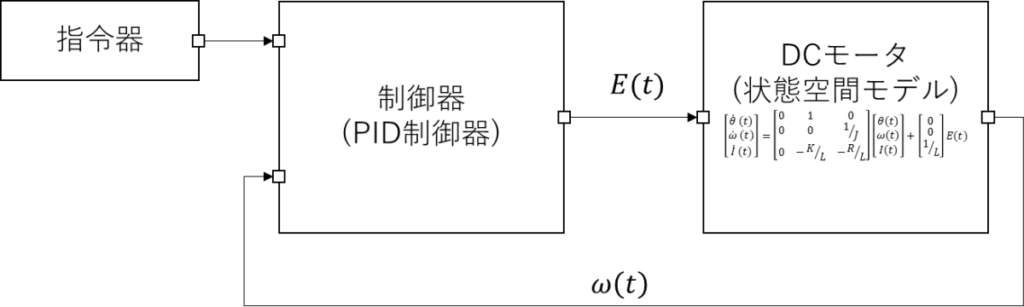
閉ループ制御（へいループせいぎょ）またはクローズループ制御（英: Close-loop control）は位置決め制御方式の一種。制御装置からの出力信号によって制御された機械やモーターの移動量のデータを制御装置にフィードバックし、入力値と出力値を常に比較して両者を一致させるように全体の操作量を調整する制御。指令だけをしてフィードバックを取らないオープンループ制御に対して、クローズループ制御は指令からフィードバックを取り補正を加える。
Wikipediaより(https://ja.wikipedia.org/wiki/%E9%96%89%E3%83%AB%E3%83%BC%E3%83%97%E5%88%B6%E5%BE%A1)

角速度\(\omega(t)\)をフィードバックしているということは角速度制御を行う体となる。