そもそもなんで決定境界直線がギリギリになるのか?
定境界直線がどこにあるべきかって話をしたが、
そもそもなんでギリギリのところになったのだろうか?
それは使用している活性化関数の影響が大きい。
ヘヴィサイド関数のことになるのだが、
この関数は入力0を境に出力0,1が切り替わる関数。
シンプルではあるのだけど、勾配が無いため、切り替わりまでの距離感がつかめない。
一応、図で示しておく。
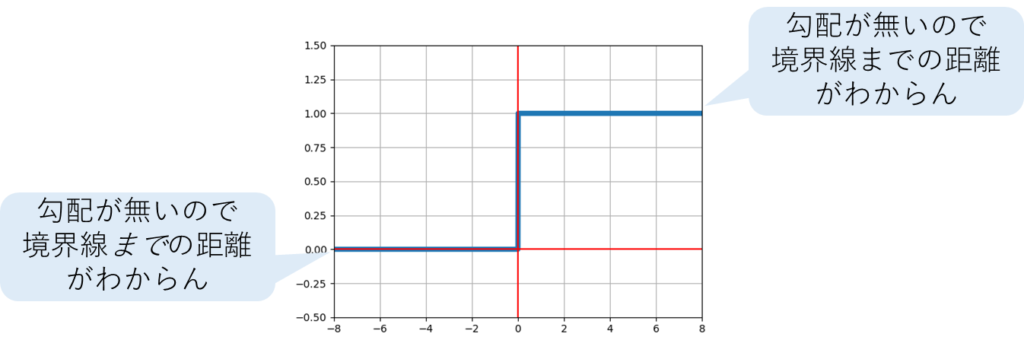
ヘヴィサイド関数は程度を表現できない?
形式ニューロンによる決定境界直線の探索は、総当たりで行った。
条件を満たすものがあれば採用、満たさなければ不採用。
というとてもシンプルなもの。
より良い条件があれば採用内容を更新ってのも可能なのだが、
ヘヴィサイド関数自体の出力の表現がないため、
より良い条件というのも探索できない。
今回はたまたま総当たりの順番の都合、外側に決定境界直線が配置されたが、
総当たり順番によっては、内側ギリギリってこともある。
条件を満たすか満たさないかの2択だから、
程度の話ができないってことになる。
というわけで、このヘヴィサイド関数を置き換える必要がある。
決定境界直線をいい感じのところに持っていくには?
決定境界直線がギリギリのところになるのは、
ヘヴィサイド関数のせいってのはわかったが、
どういった関数に置き換えれば良いだろうか?
実際に使用する活性化関数
この問題の原因は、ヘヴィサイド関数が0からいきなり1になること。
いきなり切り替わるのではなく、
じわっとした感じにすれば良いのだとう思う。
つまり、少し勾配を付ければOKなはず。
おそらくこのイメージになる。
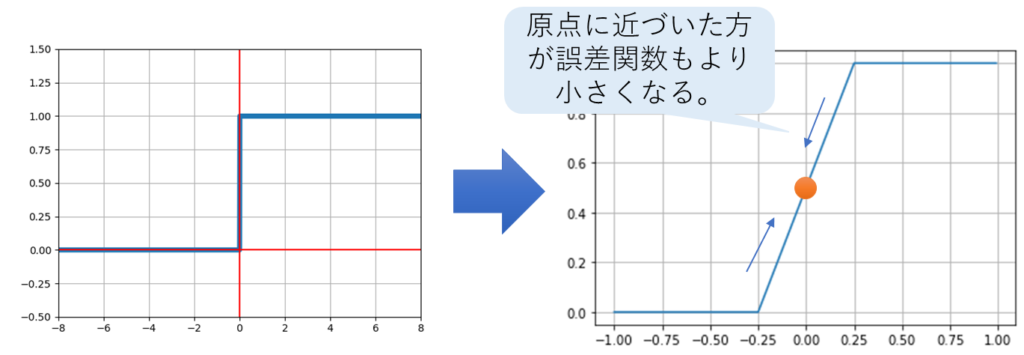
こうすると、原点に近付く方がより誤差関数が小さくなるという状況が作れる。
つまり、総当たりで確認するけど、より誤差が小さい結果があれば、それと差し替えるから、
より原点に適正な位置に決定境界直線が移動するという挙動になるはず。
実際の関数は以下と定義しておこう。
\(
\begin{cases}
y=0&(x\le -2.5) \\
y=1&(2.5\le x) \\
y=2x+0.5&(-2.5\lt x \lt 2.5)
\end{cases}
\)
この関数を便宜上、カスタムヘヴィサイド関数と名付けよう。
当然ながら造語である。
試しにこれで、いい感じの位置に決定境界直線が来るか確認してみよう。
まとめ
- 形式ニューロンのプログラムでは決定境界直線がギリギリのラインに来ていたで、どうあるべきか。について説明。
- 決定境界直線をいい感じのところに持っていくにはヘヴィサイド関数を差し替える必要がある。
- ヘヴィサイド関数の原点近辺に傾斜を付けたカスタムヘヴィサイド関数(造語)が良さげ。
MATLAB、Python、Scilab、Julia比較ページはこちら




コメント