【入門】シグモイドによる決定境界安定化(Scilab)【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
【再掲】シグモイド関数
Scilabコード
処理結果
まとめ

はじめに

の、

MATLAB,Python,Scilab,Julia比較第4章その25【シグモイドによる決定境界安定化⑤】

を書き直したもの。

活性化関数をシグモイド関数にした形式ニューロンをScilabで実現

【再掲】シグモイド関数

差し替えるシグモイド関数の数式と波形は以下になる。

\(
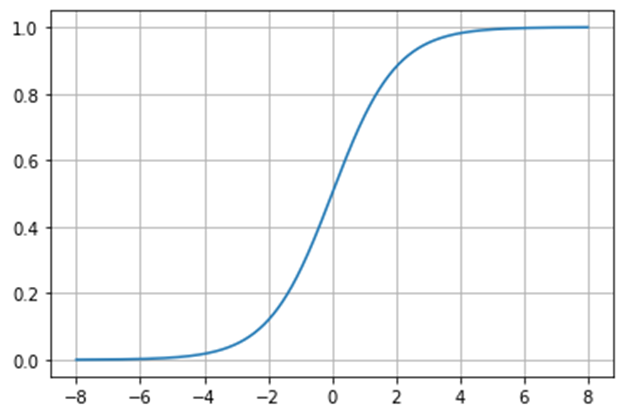
\displaystyle\varsigma=\frac{1}{1+e^{-ax}}=\frac{tanh(ax/2)+1}{2}
\)

これを活性化関数とした形式ニューロンをScilabで実現する。

Scilabコード

Scilabコードは以下

function y = sigmoid(x)
    y = 1./(1 + exp(-x));
endfunction

function NeuronalBruteForceCustomLearningHeaviside()
    // データセットの入力
    X = [0 0; 0 1; 1 0; 1 1];
    // データセットの出力
    Y = [0; 0; 0; 1];
    
    // パラメータの初期値
    W = zeros(2, 1); // 重み
    b = 0; // バイアス
    num_epochs = 10000; // 学習のエポック数
    learning_rate = 0.1; // 学習率
    min_loss = %inf;
    learning_range = 4;
    n = length(Y);
    
    // 重みの総当たり計算
    best_w1 = 0;
    best_w2 = 0;
    best_b = 0;
    for w1 = -learning_range:learning_rate:learning_range
        for w2 = -learning_range:learning_rate:learning_range
            for b = -learning_range:learning_rate:learning_range
                // フォワードプロパゲーション
                Z = X * [w1; w2] + b; // 重みとバイアスを使用して予測値を計算
                A = sigmoid(Z); // シグモイド活性化関数を適用
    
                // 損失の計算
                loss = 1/n * sum((A - Y).^2); // 平均二乗誤差
    
                // 最小損失の更新
                if loss < min_loss
                    min_loss = loss;
                    best_w1 = w1;
                    best_w2 = w2;
                    best_b = b;
                end
            end
        end
        // ログの表示
        printf('loss: %f\n', min_loss);
        printf('weight: w1 = %f, w2 = %f\n', best_w1, best_w2);
        printf('bias: b = %f\n', best_b);
    end
    
    // 最小コストの重みを更新
    W = [best_w1; best_w2];
    b = best_b;
    
    // 学習結果の表示
    printf('learning completed\n');
    printf('weight: w1 = %f, w2 = %f\n', W(1), W(2));
    printf('bias: b = %f\n', b);
    
    // 出力結果確認
    result = sigmoid(X*[W(1);W(2)]+b);
    printf('X=');disp(X);
    printf('hatY=');disp(result);
    
    // 分類境界線のプロット
    x1 = linspace(-0.5, 1.5, 100); // x1の値の範囲
    x2 = -(W(1) * x1 + b) / W(2); // x2の計算
    
    clf;
    scatter(X(Y == 0, 1), X(Y == 0, 2), 'fill','markerFaceColor','r','markerEdgeColor','r');
    scatter(X(Y == 1, 1), X(Y == 1, 2), 'fill','markerFaceColor','b','markerEdgeColor','b');
    plot(x1, x2, 'k', 'LineWidth', 2);
    p=gca();
    p.data_bounds(:,1)=[-0.5;1.5];
    p.data_bounds(:,2)=[-0.5;1.5];
    title('Decision Boundary');
    xlabel('x1');
    ylabel('x2');
    legend('Class 0', 'Class 1', 'Decision Boundary');
    xgrid;
endfunction

NeuronalBruteForceCustomLearningHeaviside()

処理結果

処理結果は以下。

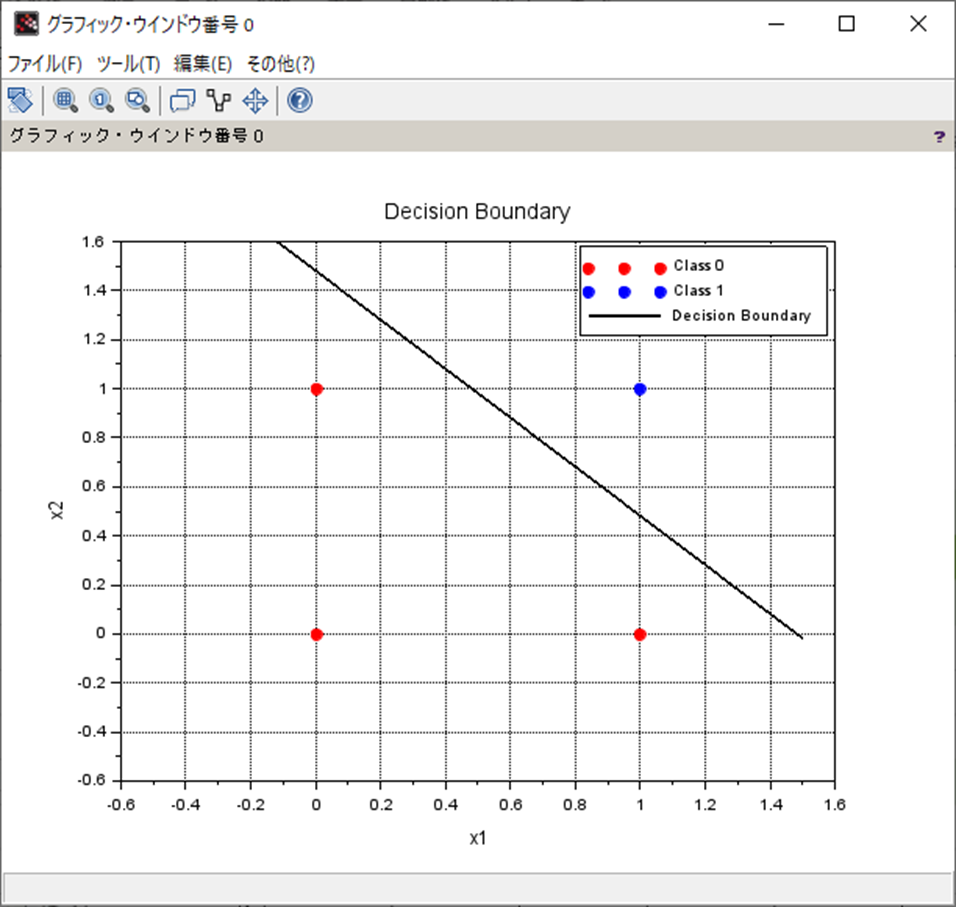
weight: w1 = 2.700000, w2 = 2.700000
bias: b = -4.000000
X=
   0.   0.
   0.   1.
   1.   0.
   1.   1.
hatY=
   0.0179862
   0.2141650
   0.2141650
   0.8021839