MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その21【シグモイドによる決定境界安定化①】
MATLAB,Python,Scilab,Julia比較 第4章 その22【シグモイドによる決定境界安定化②】
を書き直したもの。
前回まででカスタムヘヴィサイド(造語)を使用した決定境界直線の安定化を行ったが、
もっと一般的に使用される関数がある。
シグモイド関数についての説明。
カスタムヘヴィサイド関数(造語)とシグモイド関数の比較についても。
決定境界直線の一般的な安定化方法
とりあえず、カスタムヘヴィサイド(造語)ってやつで決定境界直線を安定化できたところになる。
カスタムヘヴィサイド関数・・・その名の通り、勝手に作った関数なのだが、
実は一般的に使用される関数もある。
それはシグモイド関数。
シグモイド関数
シグモイド関数はディープラニング関連でよく聞く関数だと思う。
ニューラルネットワークを学ぶ際に、
最初に知ることになる活性化関数が大体シグモイド関数だろう。
目的はヘヴィサイド関数とおおよそ一緒で。
やりたいことは「入力0を境に出力が0,1が切り替わる」になる。
しかし、それをそのまま実現するとヘヴィサイド関数の問題であった、勾配が無いってのに引っかかる。
シグモイド関数はヘヴィサイド関数と似てはいるが、常に勾配がある関数になる。
ここまでの説明だと、
前回まで使用したカスタムヘヴィサイド関数(造語)と似たようなものになるが、
カスタムヘヴィサイド関数は±2.5の0近辺に勾配を持たせたものだが、それ以外には勾配はない。
シグモイド関数は±∞の全域に勾配がある。
という違いはある。
(シグモイド関数も原点から離れるとかなり勾配は緩くなるが)
つまり、ヘヴィサイドの目的とも合致して、
カスタムヘビサイドの特性を持ちつつ
さらに全域で勾配を持ってくれる便利関数があるってことになる。
シグモイド関数の定義
シグモイド関数の定義を確認してみよう。
Wikipediaから引用する。
シグモイド関数(シグモイドかんすう、英: sigmoid function)は、次の式
\(
\displaystyle\varsigma=\frac{1}{1+e^{-ax}}=\frac{tanh(ax/2)+1}{2}
\)で表される実関数である。ここで、 \(a\)をゲイン (gain) と呼ぶ。 シグモイド関数は、生物の神経細胞が持つ性質をモデル化したものとして用いられる。
Wikipediaより(https://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%B0%E3%83%A2%E3%82%A4%E3%83%89%E9%96%A2%E6%95%B0)
シグモイド関数の式はぱっと見意味不明な感じだが、
数式自体は、そういうものなんだなって程度で覚えておけばOK。
とくに理屈のようなものはない。
理屈はないが、特性は利用するってスタンスになる。
その特性が0,1を表現可能で、全域で勾配があるというものになる。
あとは、導関数が存在するというのも重要な性質だが、
これについてはいずれ話すことになると思う。
「生物の神経細胞場持つ性質」ってあるのがニューラルネットワークっぽさを表している。
細かい経緯はわからないが、ニューラルネットワークのために生まれた関数なのかもしれない。
カスタムヘヴィサイドとシグモイドの違い
ここまでの説明でカスタムヘヴィサイドとシグモイドの差は分かったとは思うが一応図示しておこう。
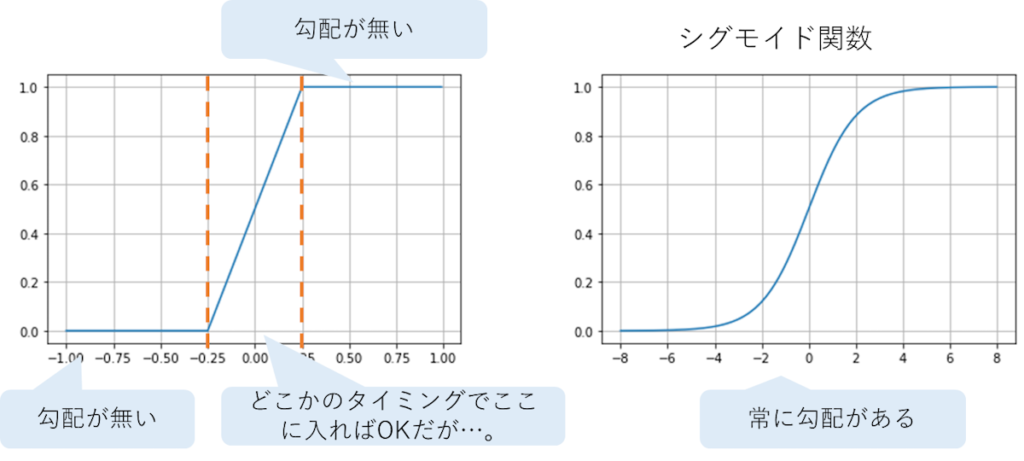
予想通りではあるとは思うが、
カスタムヘビサイドは±2.5より外側には勾配が無い。
シグモイドは常に勾配がある感じになる。
今使用している総当たり法の場合、どちらを使用しても同じ結果になるはずだが、
今後予定している誤差逆伝播法を使用し始めるとシグモイドじゃないとかなり都合が悪い。
誤差逆伝播法についても必要になったら説明しよう。
プログラム化について
一応カスタムヘヴィサイドの代わりにシグモイドを使用したプログラムを作成するが、
本当に関数を差し替えるだけになる。
よって、ソースコードは作成するが細かい考察はしない予定。
(総当たり法ではカスタムヘヴィサイドとシグモイドに効能的な差がないので・・・。)
まとめ
- 決定境界直線の一般的な安定化方法がある。
- シグモイド関数を使用する方法。
- シグモイド関数の定義について説明。
- カスタムヘヴィサイドとシグモイドの比較。
- 総当たり法では効能の差は出ないが、誤差逆伝播法を使い始めるとシグモイドじゃないと都合が悪い。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント