MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その54【単回帰分析③】
を書き直したもの。
正規方程式を用いた、単回帰分析について。
今回は、Scilabで演算してみる。
正規方程式と各パラメータ再掲
まずは正規方程式と単回帰分析に於ける各パラメータの再掲。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
単回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1 & 1\\
x_2 & 1\\
\vdots & \vdots\\
x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)
今回は、これをScilabを使用して解いてみる。
Scilabコード
Scilabコードは以下になる。
x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, ...
2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, ...
3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, ...
25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
A=[x',ones(length(x),1)];
b=y';
X=(A'*A)^-1 *A'*b;
disp(X);
xp=linspace(0, 4, 400);
plot(x, y, '+', xp, X(1)*xp+X(2), '-');
p=gca();
p.tight_limits(:)="on";
p.data_bounds(:,1)=[0;4];
p.data_bounds(:,2)=[10;41];処理結果
処理結果は以下。
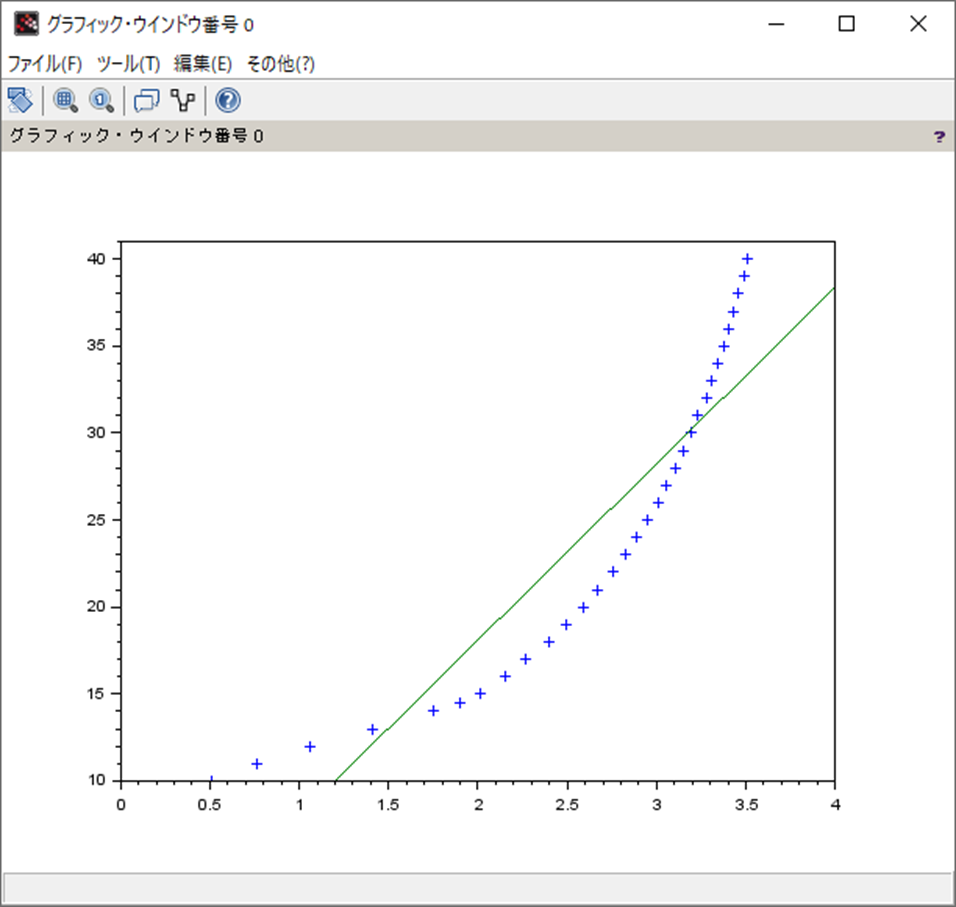
10.133034
- 2.1616644 考察
これもMATLABと同じ結果が得られた。
コードもグラフ表示部の細かい調整が違うのみで、演算部分は全く一緒
ScilabはMATLABと比較して、特に悩む部分はなさそう。
まとめ
- 正規方程式による単回帰分析をScilabで実施。
- MATLABの演算と同じ結果が得られた。
- 計算部分は全く一緒。
- グラフ表示部の微調整の仕方が違う。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント