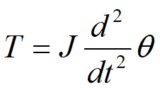【やり直し】回転運動(トルク、角運動量、仕事、仕事率)【高校物理】

はじめに
回転運動の各定義
トルクと仕事
直交座標系と極座標系の接点
まとめ

はじめに

※ 本記事は以下を親記事とした子記事に該当する。
https://www.simulationroom999.com/blog/mechanics-overview/

今回は力学の中で一番挫折者が多いと思われる極座標系こと回転運動となる。
しかし、弧度法でワンクッション置いたので何となくイメージが湧きやすくなってはいないだろうか。

回転運動はモーター関連を調べる際に避けて通れない。

回転の運動方程式がどのように使われるかの一例として以下参照。

モーター伝達関数導出(運動方程式)

ここで言う運動方程式は回転の運動方程式となる。 (モーター自身は回転運動しかしないため。) イナーシャJはローターの形状、質量から算出される定数。反力T_Lは仕事させたときに初めて確定する。

モデルベース開発とモータバックナンバー

博識フクロウのフクさんと中堅エンジニア太郎くんの「モデルベース開発とモータバックナンバー」。仕事率、エネルギー保存則。仕事率、電力。トルク、回転数。効率、損失。T-I特性、T-N特性。

上記以外にもモーターに関連する情報はモータータグから

モーター

「モーター」の記事一覧です。

回転運動の各定義

直線運動の時と似たような定義が４つある。

トルク$T[N・m]$
角運動量$L[N・m sec]$
仕事$W[J]$
仕事率$P[W]$

関係性も直線運動と似た感じになる。(速度→角速度の違いはあるが)

角運動量$L[N・m sec]$=トルク$T[N・m]$×時間$[sec]$
仕事$W[J]$=角運動量$L[N・m sec]$×角速度$[rad/sec]$
仕事率$P[W]$=仕事$W[J]$÷時間$[sec]$

ちなみに仕事と仕事率は直線運動と同じものである。
つまり、この仕事、仕事率が直座標系との直接的な接点となる。

トルクと仕事

※Google経由で「トルク仕事」のキーワードで入ってくる方々が結構いるようなので、追記。

基本的には上記の理屈をそのまま適用すればOK。

仕事$W[J]$=角運動量$L[N・m sec]$×角速度$[rad/sec]$

仕事$W[J]$= トルク$T[N・m]$×時間$[sec]$×角速度$[rad/sec]$

角度$[rad]$＝時間$[sec]$×角速度$[rad/sec]$
なので、

仕事$W[J]$= トルク$T[N・m]$×角度$[rad]$
と表現できる。

さらに後述されてる話ではあるが、
トルク$T[N・m]$ ＝力$F[N]\times$半径$r[m]$
なので、
仕事$W[J]$=力$F[N]\times$半径$r[m]$ ×角度$[rad]$

力$F[N]\times$回転半径$r[m]$ の$\times$は掛け算ではなく、クロス積(外積)な点に注意。
クロス積(外積)なので、以下の表現もできる。

仕事$W[J]$=力$F[N]$ × 回転半径$r[m]$ × $sin\theta$×角度$[rad]$

$sin\theta$ が90°、
つまり、力$F[N]$ の向きが回転半径$r[m]$ と直交していることを前提に出来る場合は
$sin(90°)$ =1
となるため、上記式から $sin\theta$ が消える。

たぶん、ここらへんの表現の豊富さにやられて皆さんググってこられているのでしょう。

全体の関係性は本記事下部の表を見ることでつかめると思う。

あとは、トルクと仕事の単位が似ているというのも混乱を誘っているかもしれない。

トルクの単位は$[N\cdot m]$
仕事の単位は $[Nm]$

共に力の単位$[N]$と距離の単位$[m]$を掛けたものに見える。
が、別物を思った方が良い。
トルクの単位の$[N\cdot m]$は暗黙的に$sin(\theta[rad])$ が隠れているのと、
距離の単位$[m]$ は移動距離ではなく、回転運動の半径を示しているため全く意味が異なる。
まぁその違いを示すために「$ \cdot $」が入ってるのでしょうけど。