はじめに
※ 本記事は以下を親記事とした子記事に該当する。
https://www.simulationroom999.com/blog/mechanics-overview/
前回、直交座標系こと直線運動の説明をした。
このままの勢いで極座標系こと回転運動に突入したいが、その前に弧度法について説明する。
結論としては、「弧度法は難しいものでなく、計算をサボるための便利な表現」になる。
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%B8%E3%82%A2%E3%83%B3
弧度法
角度の表現には2つの表現方法がある。
- 度数法
- 30[°(度)]という表現
- \(360[°]\)で一回転
- 弧度法
- 30[rad(ラジアン)]という表現
- \(2π[rad]\)で一回転
一般的には度数法の方が有名であるが、力学では弧度法を使用する。
弧度法の単位はラジアンと呼ばれ、\([rad]\)と表現される。
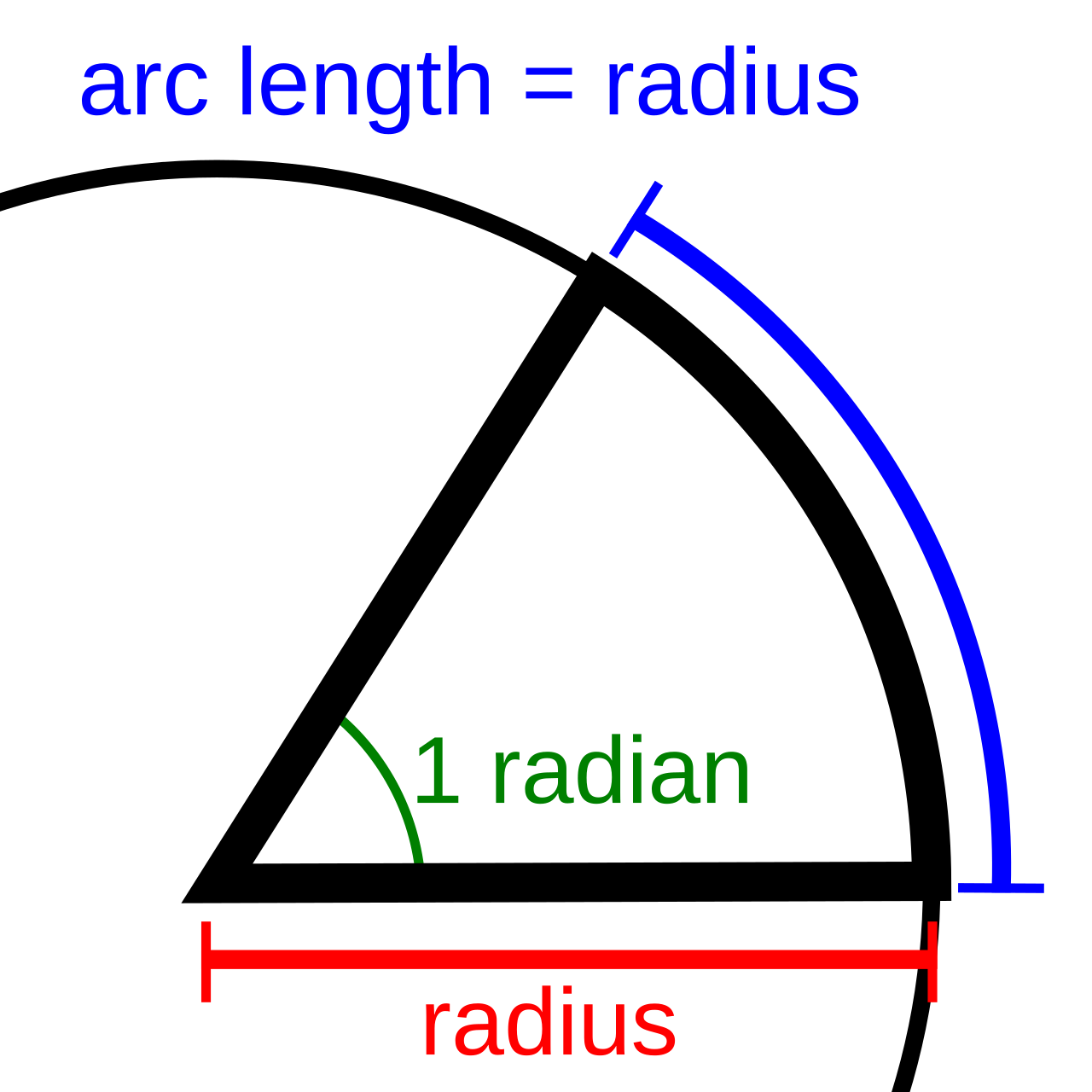
\(1[rad]\)は、
円の半径に等しい長さの弧の中心に対する角度
計量単位令による定義
となる。
円周は\(2πr\)であるため、一周は\(2π[rad]\)となる。
また、半径\(3[m]\)の車輪が角度\(2[rad]\)回った場合の移動距離はラジアンの定義により、
$$3[m]×2[rad]=6[m]$$
となる。
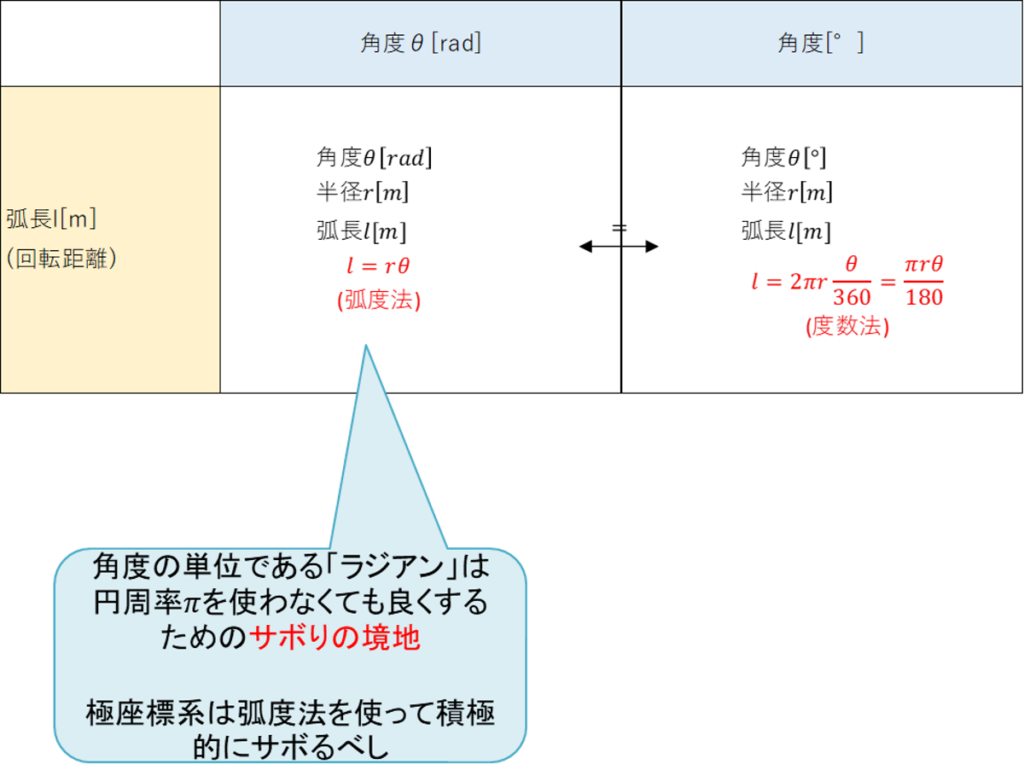
重要なのが後者で、半径と弧度法としての角度が分かっていれば、単純な掛け算で円周が表現できる。
これが度数法だと、
$$2πr[m]\frac{θ[°]}{360[°]}=\frac{πr[m]θ[°]}{180[°]}$$
となり、かなり煩わしい。
つまり、弧度法とは、回転運動の際にこの煩わしさから解放してくれるテクニックと言うことになり、端的に言うと昔の偉い人達が考えてくれたサボりの境地である。
まとめ
回転運動を扱う際は度数法ではなく、弧度法を使って積極的にサボろう。
大学入試 漆原晃の 物理基礎・物理[力学・熱力学編]が面白いほどわかる本
大人のための高校物理復習帳 役立つ物理の公式28 (ブルーバックス)
はじめて学ぶ物理学—学問としての高校物理(上)
はじめて学ぶ物理学—学問としての高校物理(下)




コメント