プログラミングの前に?
前回の数式を元にプログラミング・・・なのだが、
その前に数式を変形しておく必要がある。
アフィン変換の時もそうだったのだが、
今回やってる射影変換は、厳密には射影逆変換。
つまり、渡す変換行列に細工が必要。
実際の数式
射影逆変換を想定した数式は以下になる。
\(
\begin{eqnarray}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}&=&
\begin{bmatrix}
a&b&c\\
d&e&f\\
g&h&1
\end{bmatrix}^{-1}
\begin{bmatrix}
S_x&0&0\\
0&S_y&0\\
0&0&1
\end{bmatrix}^{-1}\\
&&\begin{bmatrix}
1&0&T_x\\
0&1&T_y\\
0&0&1
\end{bmatrix}^{-1}
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)&0\\
\sin(\theta)&\cos(\theta)&0\\
0&0&1
\end{bmatrix}^{-1}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\end{eqnarray}
\)
逆行列にして、実施した順番になれべればOK。
ここらへんの証明は以下で実施済み。
忘れているならば、復習しておくと良いだろう。
実際のパラメータ
変換時のパラメータも決めておく必要がある。
とりえあずテキトーに決めてしまおう。
射影変換
\(
\begin{eqnarray}
(-1,-1)→&(-0.5,-0.8)\\
(-1,1)→&(-0.8,0.8)\\
(1,1)→&(1,1)\\
(1,-1)→&(0.4,-1)\\
\end{eqnarray}
\)
伸縮アフィン
縦横を1/2へ縮小
移動アフィン
x軸方向+0.5
回転アフィン
+60°
どんな感じの画像になればOKなのか?
先ほどのパラメータを使用した場合、どのような結果になるかを予測しておこう。
想定としては以下になると思ってる。
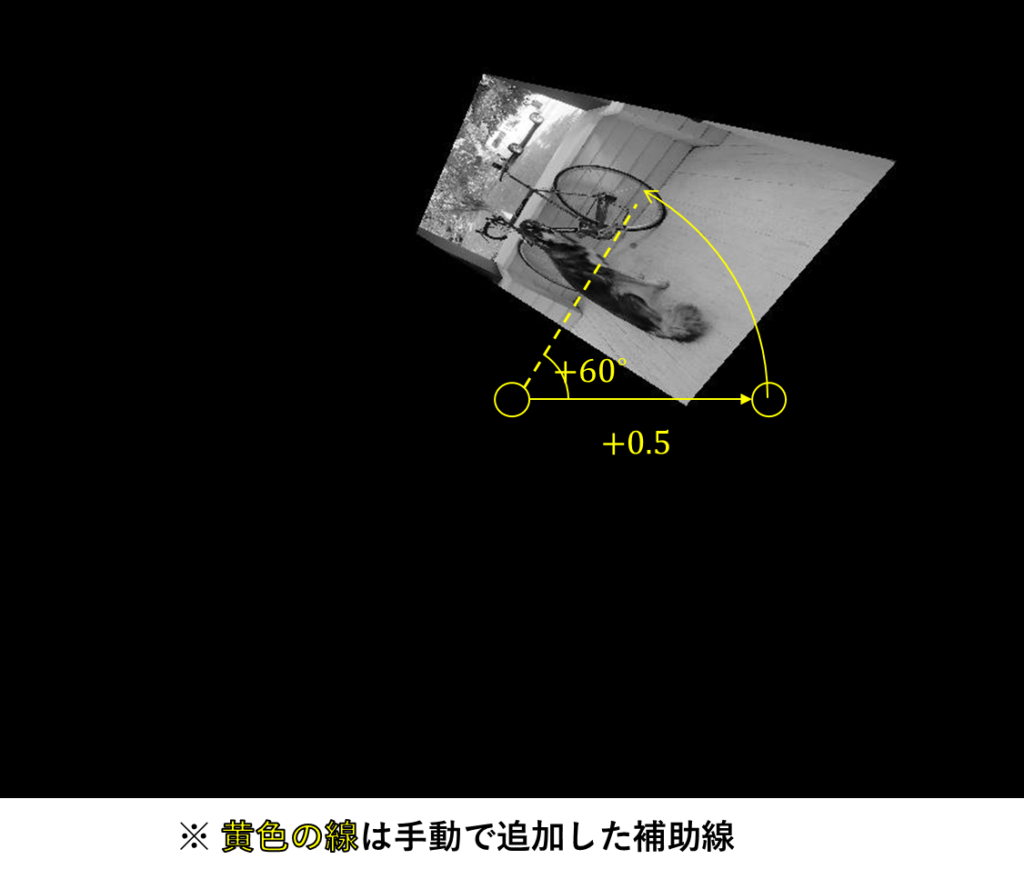
補助線も入れているので、プロセスもわかると思う。
最終的にはこんな感じになればOK。
まとめ
- 射影変換は数式上はアフィン変換の拡張型。
- 射影変換のアフィン行列を入れてアフィン変換になるか試そうと画策。
- 射影変換、アフィン変換合成時のパラメータを(テキトーに)決めた。
MATLAB、Python、Scilab、Julia比較ページはこちら






コメント