分類の推移を見てみる
いろいろ表現方法を試行錯誤して、
原因特定用の情報はそろった状態、
先の同じく、成功パターンと失敗パターンに分けて見てみる。
分類成功パターン
分類成功パターンの決定境界線と誤差関数の推移は以下になる。
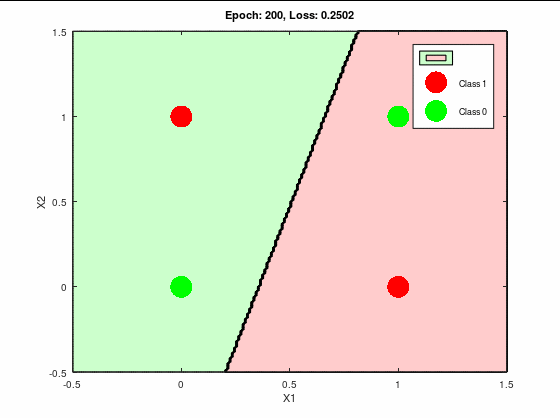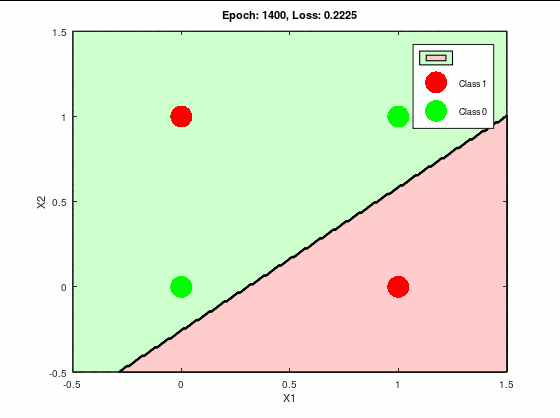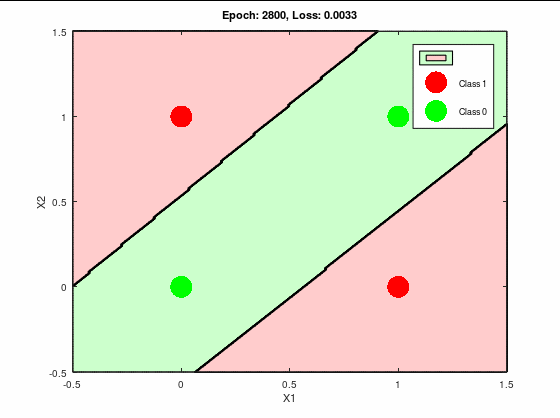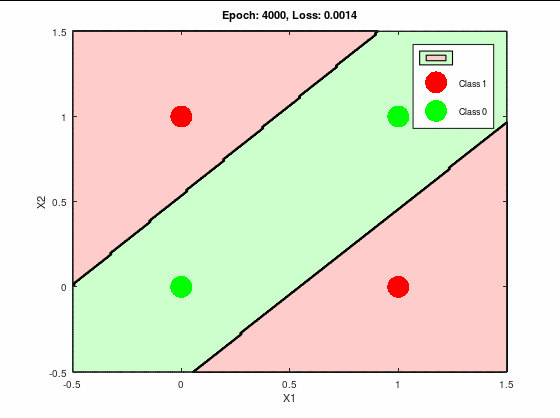
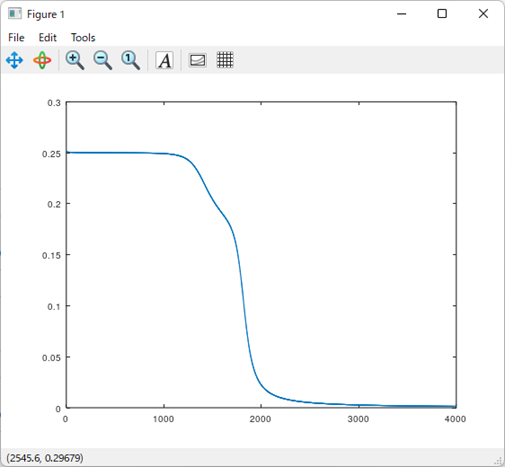
これはキレイに推移してる。
誤差関数もほぼ0へ収束している。
理想的な推移と言って良いだろう。
分類失敗パターン
次は問題の分類失敗パターン。
決定境界線と誤差関数の推移は以下になる。
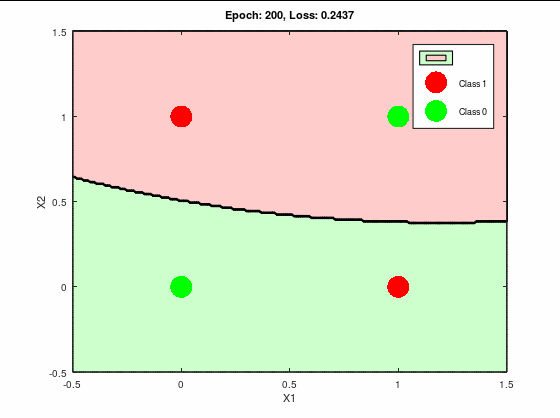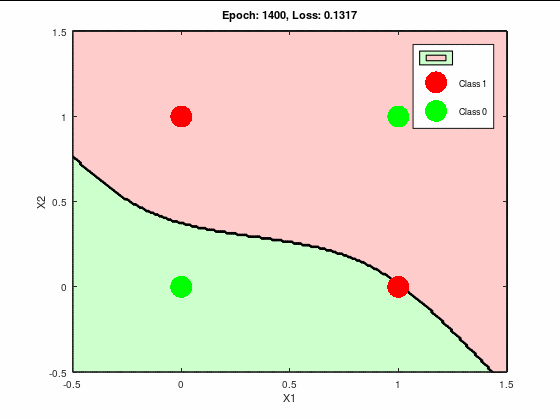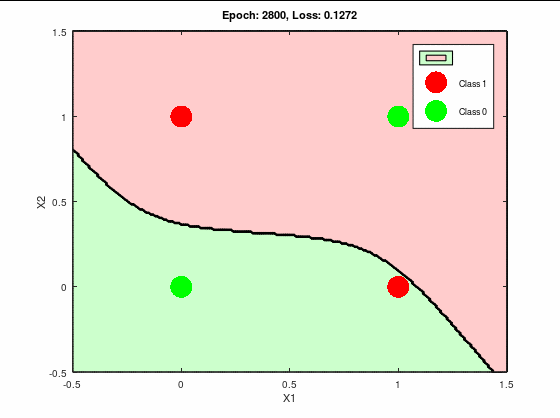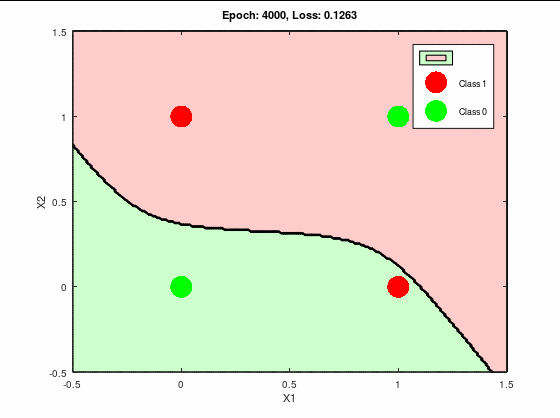
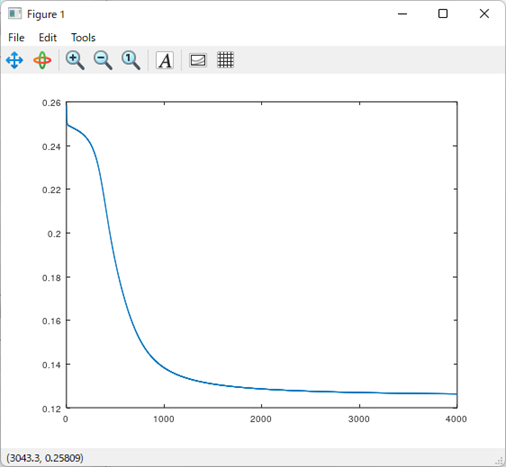
これは完全に失敗している。
誤差関数としては収束はしているが、
0には至ってない。
つまり局所最適解にハマってる。
これはエポック数を増やしても解決するものではないだろう。
というわけで、推移が見えれば原因も分かり易くなるってことになる、
対策
対策についてだが、
大きく2つある。
- 隠れ層のユニット数を増やす
- 勾配降下法を拡張した最適化アルゴリズムを採用する
一個目はシンプル話ではあるが、
二個目が少々解説が必要な話になる。
結論としては一個目で対策可能なはず。
二個目はもっと複雑なネットワークな場合に有効な手法になる。
というわけで、一個目だけやれば対策としては終了となるはず。
しかしせっかくなので二個目についてもやってしまおうと思う。
どういう最適化アルゴリズムがあり、どのような効果が期待できるかは知っておいた方が良いと思う。
AI技術としては一般的な話なので、ネットワークがシンプルなときにやっておいた方が分かり易いだろう。
まとめ
- 非線形分類をしたが実は問題が発生している。
- 非線形分類が失敗する原因を特定するため決定境界線と誤差関数の推移をモニタ。
- 案の定、局所最適解にハマってる。
- つまりエポック数を増やしても対策にはならない。
- 隠れ層のユニット数を増やす、最適化アルゴリズムを使用するのが対策案。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント