微分
そして微分。
おそらく、微分アレルギーな人は多いと思う。
応用範囲の広い手法であり、
微分が難しいというよりも、難しい問題に適用されることが多いため、
どうしてもアレルゲンになりやすい・・・。
微分の具体的な利用シーンは先ほどの一次関数の利用シーンとおおよそ重複。
一次関数は認識しやすい、大雑把な表現に対して、
微分は、その瞬間の増減とその割合を示すことができる。
まぁ、この「その瞬間の」って言い回しが魔境臭半端ないのだが・・・。
微分は、ある関数のある点の接線の傾きって言われている。
そして、その接線は必ず一次関数ということになる。
というわけで、微分は、ある関数のある点に於ける変化の割合であり、x軸の次元を削除したものともとれる。
まずは、微分の近似である数値微分を見てみる。
以下ような関数があり、この点の変化の割合を確認したい。とする。
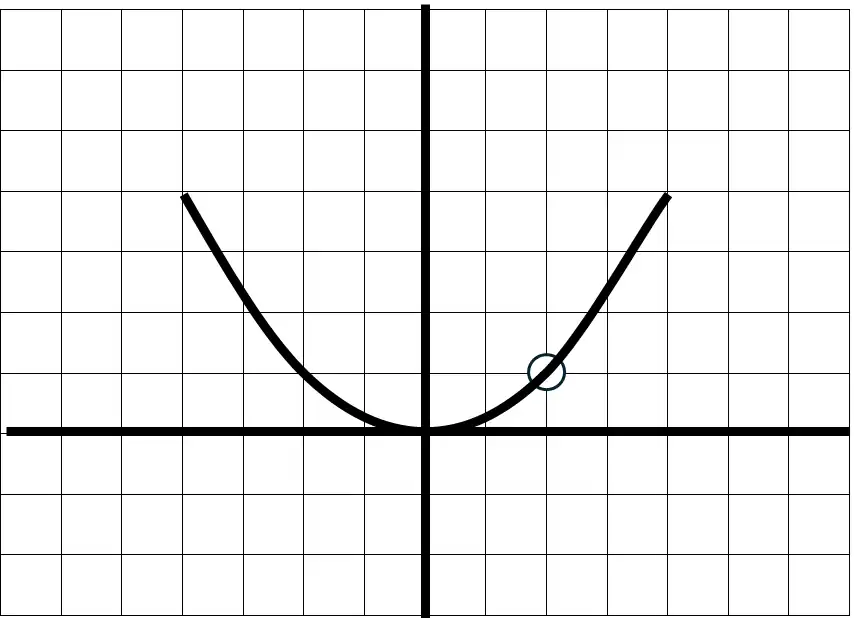
とりあえず、その点を(x,y)とし、そこより少し右の点を(x’,y’)とする。
(x,y)から(x’,y’)を引いたものが(Δx,Δy)。
接線に近似した傾きはどのように表現されるか。
この場合、最も小さい変化はΔxとΔyになる。
そして傾きということから、Δy/Δx
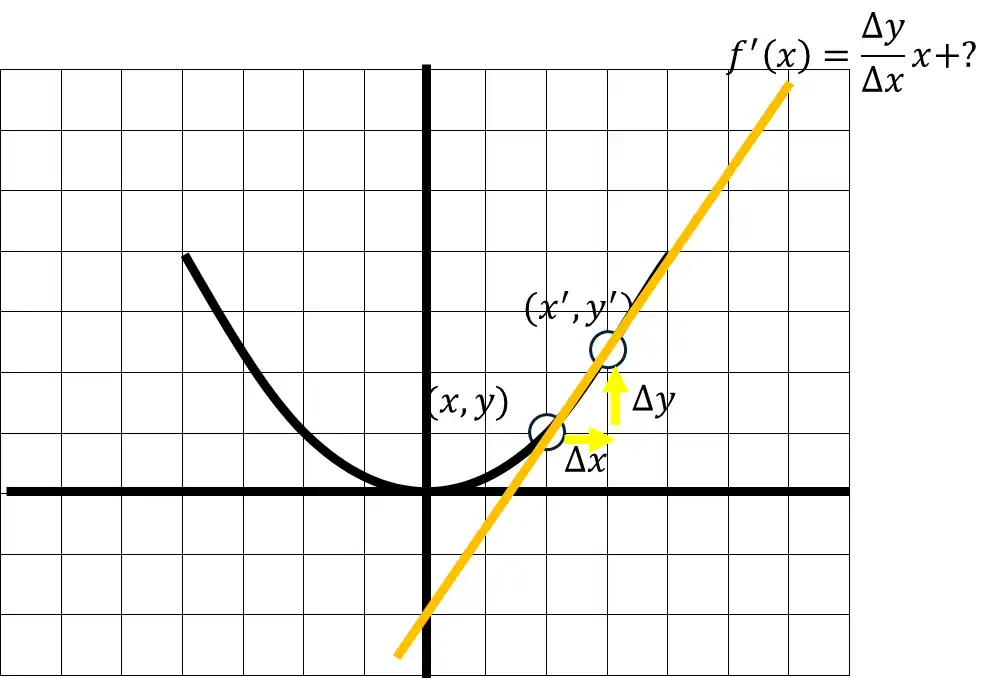
\(
\displaystyle f^\prime(x)=\frac{\Delta y}{\Delta x}+?
\)
これが数値微分というもので、未知の関数に対して微分の近似を求める手法になる。
近似ということから、微分そのものではないとも言える。
実際の微分は、Δxを限りなく0に近づけるという表現になる。
本来だとこのように表現される
\(
\displaystyle f^\prime(x)=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
\)
ちなみに、先ほどのΔyはこの部分。
\(
\Delta y=f(x+\Delta x)-f(x)
\)
代入すると、極限はあるものの、さっきの式に戻る。
\(
\displaystyle f^\prime(x)=\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}
\)
f(x+Δx)-f(x)が意味わかんねぇって思われやすいが、
単なるΔyと思えば少しは気が楽になると思う。
Δxを0に近づけると、合わせてΔyも減っていくから、ΔxとΔyの割合を表す分数としての関係性は崩れない。
今回のような2次関数の場合は、Δxが小さければ小さいほど、xの点に於ける増減の割合の精度が上がっていく。
究極的には0にすれば最大精度だが、0を代入すると0除算になってしまう。
0除算は禁止されているため、極限が使用されている。
実際の微分はもっといろいろな解釈や表現があるのだが、
ここでは分数との兼ね合いにおける微分という位置付けとなる。
まとめ
- 分数は割り算の別表現として理解しやすく、逆数を掛けることで計算が簡単になる。これにより、小数の掛け算や割り算の理解が深まる。
- 一次関数の数式をグラフにすることや、グラフから数式を導くことは、データのトレンド分析や物理現象の理解に役立つ。
- 微分は関数の変化率を求める手法であり、数値微分を使って近似的に求めることができる。これにより、物理学や経済学など多くの分野で応用可能。
小学5年生約分・通分をする分数の計算 (くもんのにがてたいじドリル 算数 7)
いっきに極める算数小学4~6年の分数の計算
解法のエッセンス/関数・座標編
1次関数で学ぶ経済学 改訂版
ふたたびの微分・積分
東京大学の先生伝授 文系のためのめっちゃやさしい 微分積分



コメント