親子で発見！学びの楽しさ#2(分数、一次関数、微分)

一次関数

次は一次関数。

一次関数と分数の関連性、一次関数と微分の関係性がわからないかもしれない。
これは、一次関数の傾きの話が分数や微分と紐づく。

中学生に於いての一次関数の扱いは以下の2パターン。

中学生のことにこれをひたすらやらされ意味不明だったという人もいるかもしれない。

数式をグラフ、グラフを数式にすることは、現実世界においてはいろいろ役に立つ。

これらは、使わなくても感覚的に把握できるものでもある。
まぁ、感覚的に把握できるのも、
一次関数の数式とグラフの関係性を認識しているからできていることなのかもしれないが。
足し算、引き算、掛け算、割り算みたいに反射的に近いレベルで使ってる可能性はある。

そして、どのような感じで分数と関係してくるのか？
それは、数式、グラフを扱うとわかると思う。
まずはこの数式を元にグラフを書く。

\(
\displaystyle f(x)=\frac{2}{3}x+2
\)

この数式の意味は、傾きが2/3、切片が2。

まず、切片を元にxが0の時のプロットをする。
傾きが2/3だから、右方向に3、上方向に2の位置にプロット。
それぞれのプロットを直線で結ぶ。
以下のようなグラフになる。

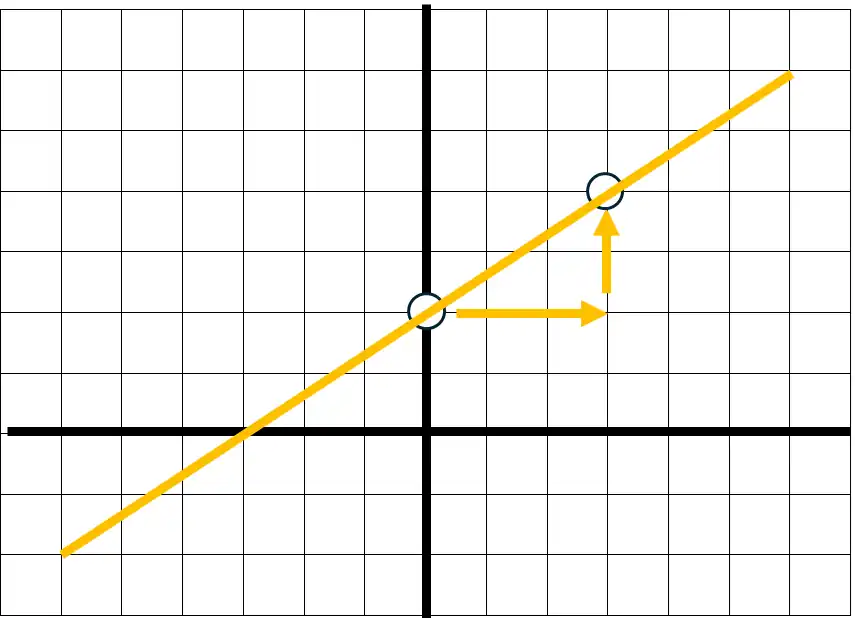
ちなみに、傾きは増加の割合なので、
右方向に6、上方向に4の位置にプロットしても同じ結果になるし、
なんだったら、右方向に1.5、上方向に1でも同じ結果になる。

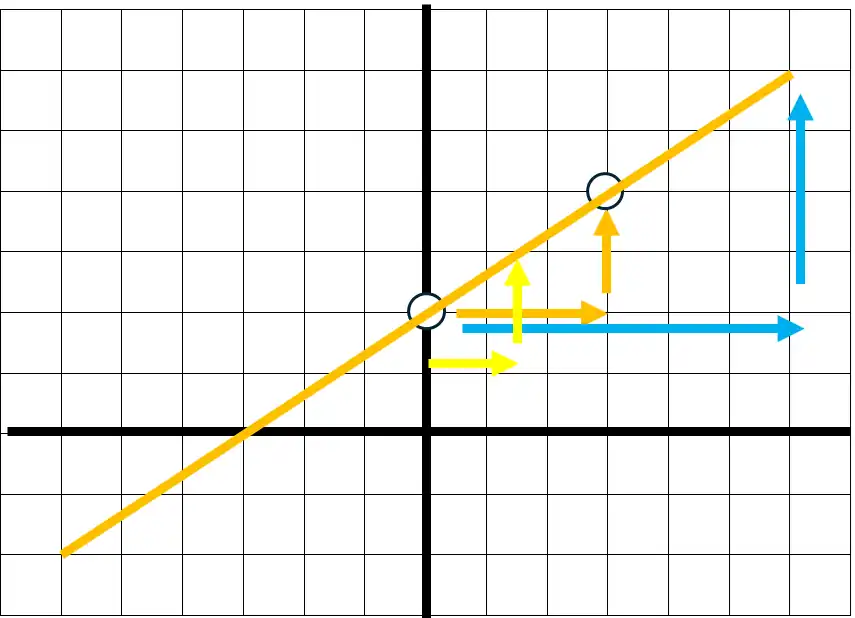
次はグラフから数式。
このグラフを数式にする。

まず、x=0を見ると、1だから、切片は1。
傾きは、右に2、上に3あたりがちょうど良さそう。
念のため、右に4、上に6を見ても一致しているから、3/2で問題ないはず。
よって、数式は3/2x+1。

\(
\displaystyle f(x)=\frac{3}{2}x+1
\)

「念のため、右に4、上に6を見る」
というのは割と重要。
問題として出されるものであれば、そこまで意地悪なものも出ないとは思うが、
一般的には微妙なズレのようなものが発生する。
よって、より大きい範囲で見た方が精度が高い傾きを得られる。
あまり意識していなかったが、地味に分数的な発想が入っている。

ちなみに、一次関数の傾きは、xが1増えるたびに増加する値でもある。
つまり、変化の割合となり、xの次元を削除したものが傾きとも言える。
この点を覚えておくと、次の微分で少し楽になる。