MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その30【三角関数の直交性⑤】
MATLAB,Python,Scilab,Julia比較 第5章 その31【三角関数の直交性⑥】
を書き直したもの。
フーリエ係数に至る道。
今回は三角関数の直交性の話のまとめ。
【再掲】フーリエ係数に至る道
まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数
今回は三角関数の直交性の話のまとめ。
三角関数の直交性のまとめ
過去三回に渡っての話で、
結論としては以下の式が得られたことになる。
\(
\begin{eqnarray}
&&\displaystyle\int_{-\pi}^{\pi}\sin(mx)\cos(nx)dx=0\\
&&\displaystyle\int_{-\pi}^{\pi}\sin(mx)\sin(nx)dx=
\cases{
\pi\dots \text{if } n=m\\
0\dots\text{if } n\neq m
}\\
&&\displaystyle\int_{-\pi}^{\pi}\cos(mx)\cos(nx)dx=
\cases{
\pi\dots \text{if } n=m\\
0\dots\text{if } n\neq m
}
\end{eqnarray}
\)
言葉としてまとめると以下になる。
- \(\sin,\cos\)は必ず直交。
- \(\sin,\sin\)は角周波数が異なる場合は直交。
- \(\cos,\cos\)は角周波数が異なる場合は直交。
- \(\sin,\sin\)、\(\cos,\cos\)は同一の角周波数の場合は\(\pi\)となる。
この概念はフーリエ級数をベクトルとしてとらえ、
フーリエ級数の中にあるフーリエ係数を取り出すために使用する。
ちょっとアニメーション
ここで、各三角関数の畳み込みの状態をアニメーションgifしてみた。
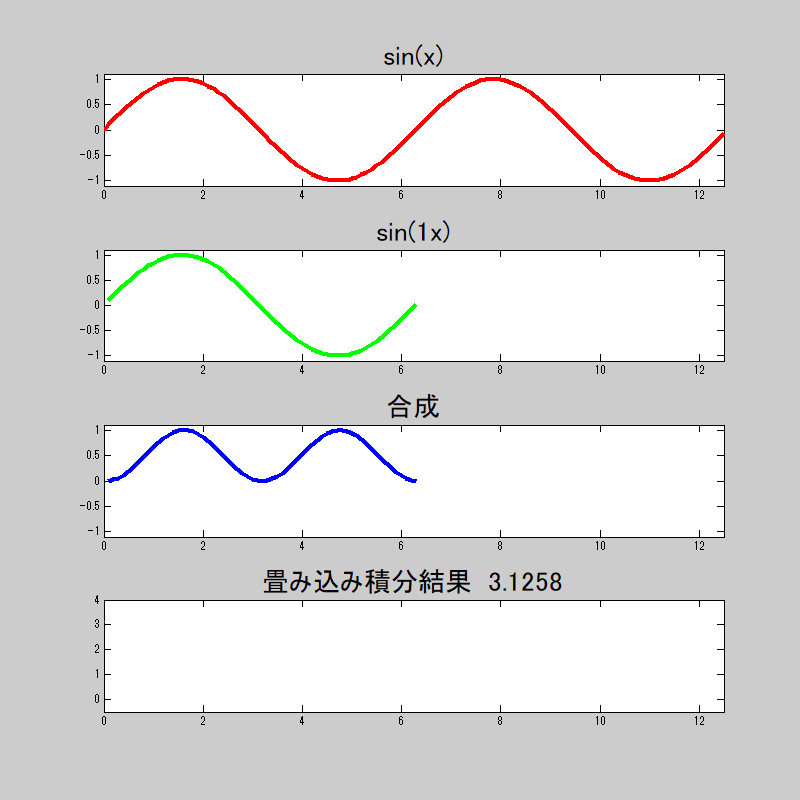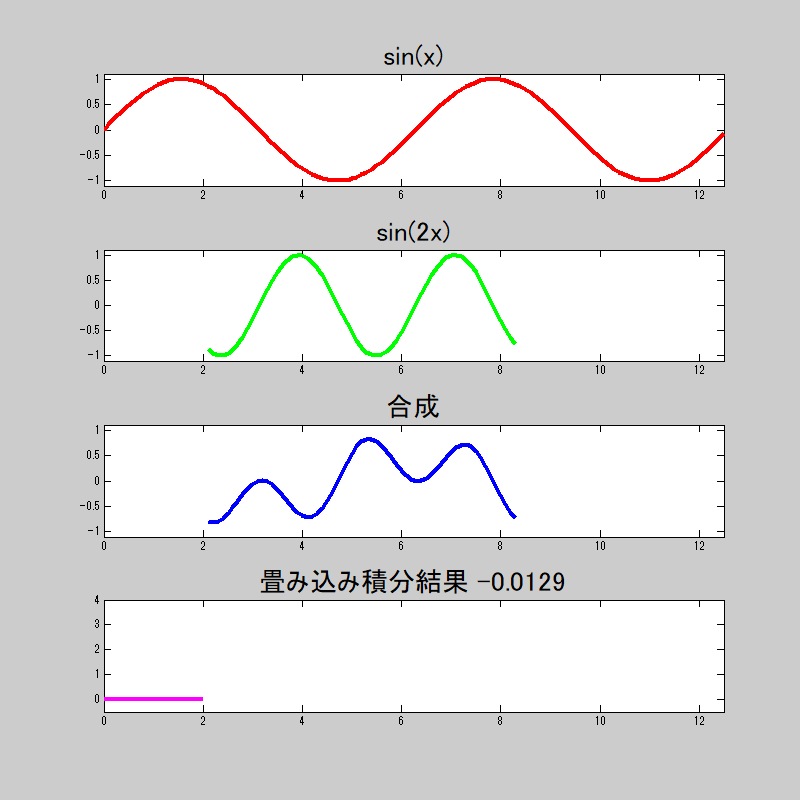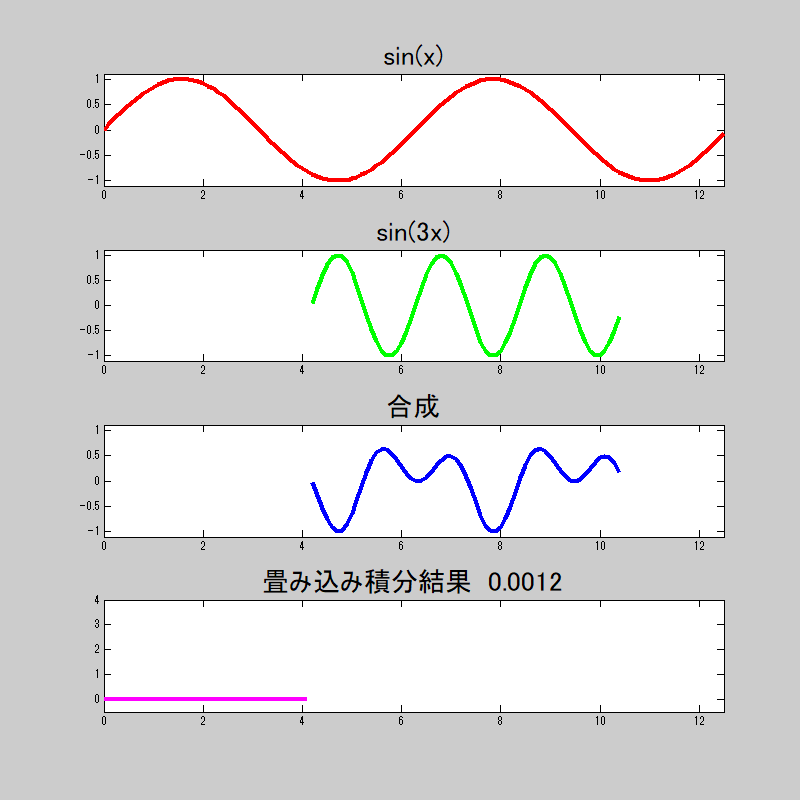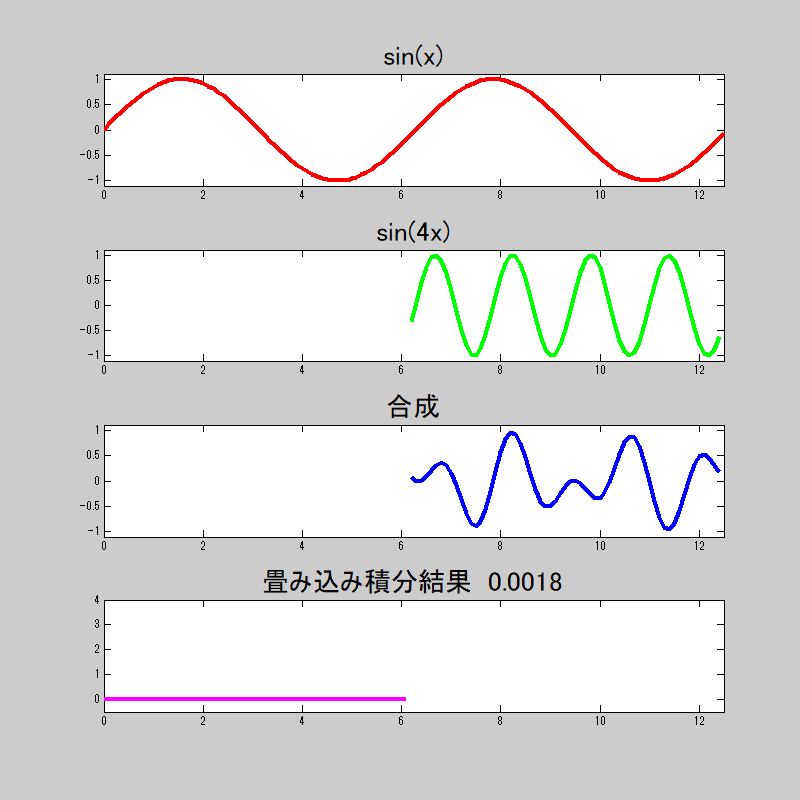
若干演算誤差はあるが、\(n=1\)の時のみ\(\pi\)に近似し、
それ以外は\(0\)に近似している。
こうやってみると割と面白い。
今後について
三角関数やその他関数の畳み込みについては、これから散々やることになる。
よって、ここらへんで一旦プログラムによる確認をやっておこうと思う。
\(0\)になるとか\(\pi\)になるとかは説明できたつもりではあるが、
実感に繋がりにくい話でもある。
そこを一回プログラムで確認できると実感できるような気がする。
その実感を得るのを目的としてやってみようと思う。
内容としては以下を求めるプログラムを想定している。
- \(\sin(x)\cdot\cos(x)=0\)
- \(\sin(x)\cdot\cos(2x)=0\)
- \(\sin(x)\cdot\cos(x)=\pi\)
- \(\cos(2x)\cdot\cos(2x)=\pi\)
- \(\cos(x)\cdot\sin(2x)=0\)
- \(\sin(x)\cdot\cos(2x)=0\)
一応、想定する結果も記載しているが、
実際のところは演算誤差は出ると思う。
よって、そこも含めて確認ということになる。
まとめ
- 三角関数の直交性のまとめ。
- 各種式を確認。
- 直交性具合をアニメーションで確認。
- 三角関数の畳み込みをプログラムでやっている予定。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント