【入門】モーメンタム③【数値計算】

モーメンタムの動作イメージ

モーメンタムの動作イメージについて

モーメンタムの動作イメージはなかなか表現しずらいが、
こんな表現になる。

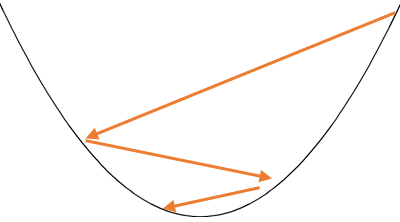
基本的には最初は大きく動いて、収束するにつれて更新値が小さくなる。
これは過去の勾配がどれだけ大きいかに依存した動きになる。

つまり、
最初は恐らく勾配が大きいから、大き目に動く。
その内、最適解に近付いてくるから、その段階で更新値が小さくなって、
細かい最適解を見つけてくれるって感じになる。

学習率自体は固定なのだが、
更新値は状況に応じて可変。
これは勾配降下法の観点で見ると学習率が状況に応じて可変と同義になる。

学習率が固定だと、適正な値を探す必要があったが、
モーメンタムだとある程度自動で変化するってことになる。
少なくとも最初は大きく動くから最適解までの収束ステップは少なくなるはず。

シンプルな更新式ではあるが、
効果は大きい。
とりあえず、まず試しても良いレベルのお手軽さだろう。

まとめ

• モーメンタムの更新式について確認。
  • 指数移動平均を利用して直近の値を重視する。
• モーメンタムの動作イメージについて確認。
  • 最初は大きく更新して、最適解が近いと小さく更新。
  • 勾配降下法で言うところの学習率が可変と同義な動きになる。

MATLAB、Python、Scilab、Julia比較ページはこちら

【入門】MATLAB,Python,Scilab,Julia使い方比較【数値計算プログラム】

MATLAB,Python,Scilab,Juliaを比較。基本的な計算、ベクトル行列演算、グラフ(波形)表示、伝達関数、画像取り込み、最小二乗法を元に比較しています。それぞれツールの特性が理解できれば使い分けも移行も難しくは無いでしょう。似ている部分も多いので私の場合はそれを利用するして実験の幅を広げています。

www.simulationroom999.com

2020.04.12

Pythonで動かして学ぶ！あたらしい線形代数の教科書

Amazon.co.jp

amzn.to

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

Amazon.co.jp

amzn.to

ゼロからはじめるPID制御

https://amzn.to/3SvzuyR

amzn.to

OpenCVによる画像処理入門

https://amzn.to/498ZUgK

amzn.to

恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]

Amazon.co.jp

amzn.to

Pythonによる制御工学入門

Amazon.co.jp

amzn.to

理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析

https://amzn.to/3UAunQK

amzn.to