MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その112【最適化アルゴリズム⑪】
を書き直したもの。
前回までで各ツール、各言語による最適化アルゴリズムAdamを試したところ。
Adamならではの分類結果が出てきたのでそれの確認を行う。
Adamならではの結果
一応、Adamの動作も確認できたから一通りやり切ったって感じになる。
今回は、Adamならではの分類が出てきたのでそれを確認しておこう。
勾配降下法やモーメンタムでは見れなかった分類結果になる。
該当の決定境界は以下になる。
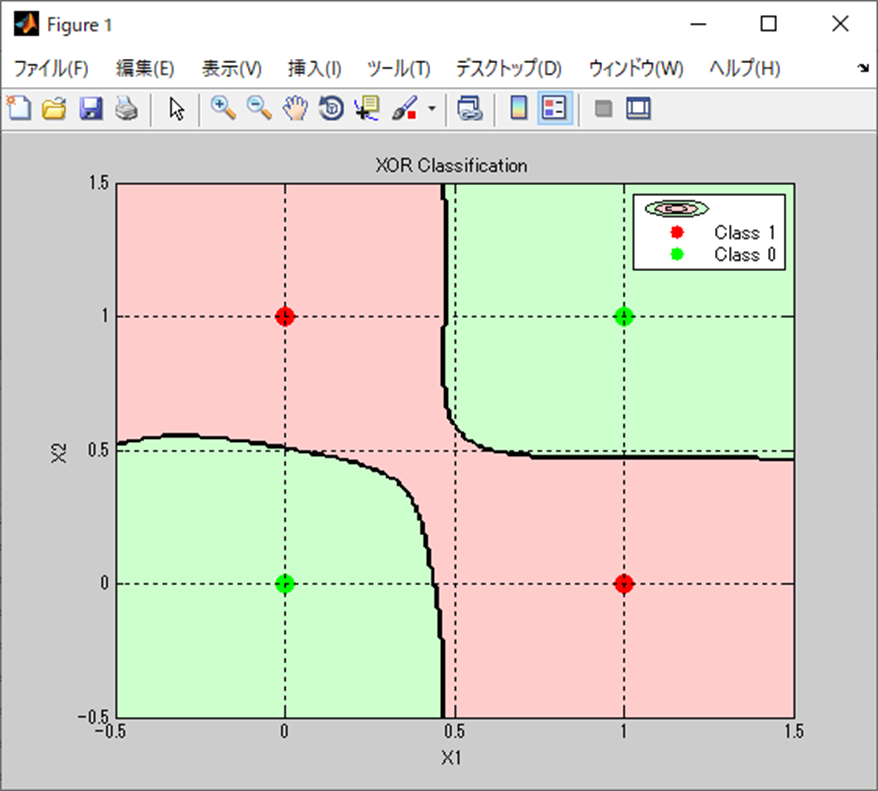
今までは、斜めに分ける感じがほとんどだったのに対して、
Adamでは4つの四角で分類された感じで、
これはこれでキレイな分類って感じになっている。
Adamの分類をアニメーションで。
分類の過程をアニメーションgifにしてみた。
そのgifを張っておこう。
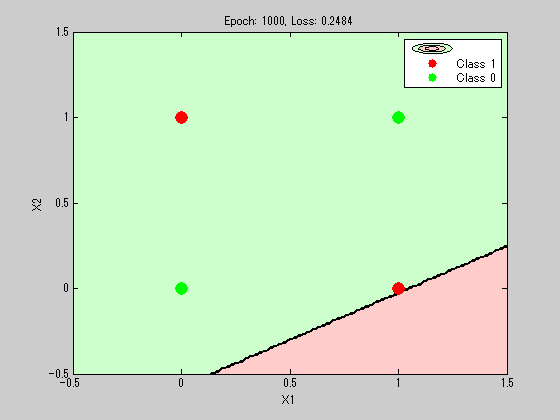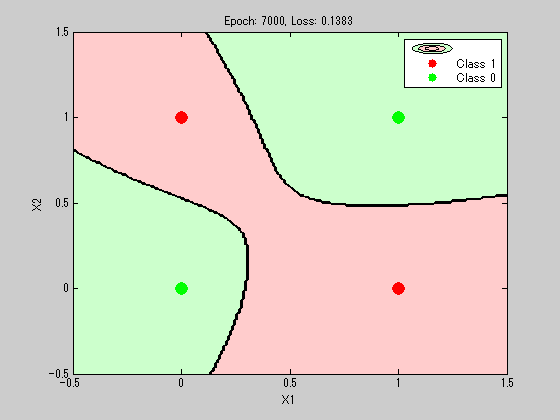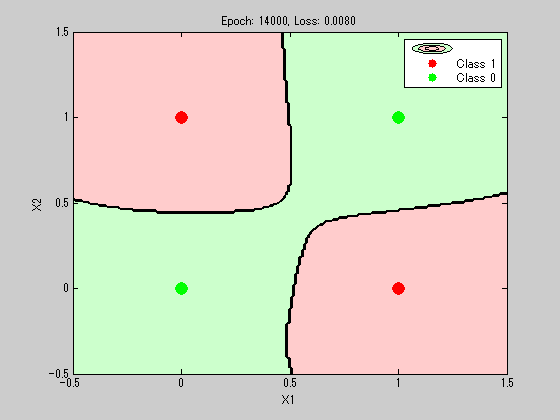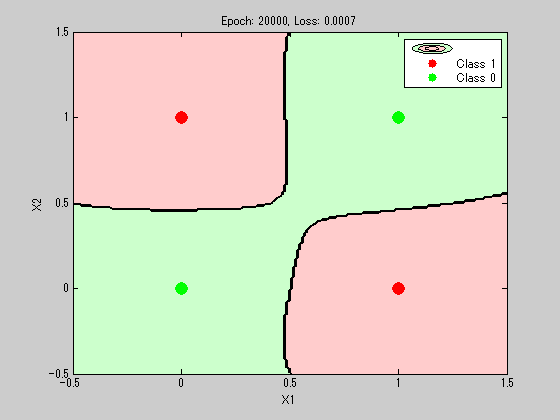
最初は単純に直線分類しようとしてるが、
それが難しくなった際に別のセグメントを引っ張り出している。
あとは、可能な限り各点から離れた位置に決定境界線を引けるように学習している感じになる。
しかし、Adamだけなぜこんなのが出てきたんだろうか?
明確にはわからないが、
誤差関数の値は通常だと0.25あたりと開始として、
そこから徐々に落ちてくるのが勾配降下法とモーメンタムの挙動だった。
対して、Adamが今回のような結果を出すときは、一旦0.4まで跳ね上がってるというのはある。
これの影響で大域最適解に至れるルートを見るけられたというのはあるかもしれない。
大域最適解を特定するもの単純にはいかないってことだと思う。
これがもっと複雑なネットワークになった際に、Adamのこの特性が強く利いてくるのだと思う。
まとめ
- Adamだけで出てくる分類結果を確認。
- 四角形で分類する理想的な形状。
- この分類結果になる場合は、誤差関数の値が一気に跳ね上がる時。
- これにより大域最適解を引き当てやすくなる。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析





コメント