【入門】最適化アルゴリズム③【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
最適化アルゴリズムいろいろ【再掲】
各最適化アルゴリズムの依存関係
Adamの更新式【再掲】
プログラムフロー
パイパーパラメータについて
まとめ

はじめに

の、

MATLAB,Python,Scilab,Julia比較第4章その107【最適化アルゴリズム⑥】
MATLAB,Python,Scilab,Julia比較第4章その108【最適化アルゴリズム⑦】

を書き直したもの。

Adamに至るまでの最適化アルゴリズムの系譜の説明をした。
今回は全体としての依存関係についての説明と、
Adamをプログラムで実現するための準備をする。

最適化アルゴリズムいろいろ【再掲】

まずは説明予定の最適化アルゴリズムを再掲。

AdaGrad(済)
RMSprop(Root Mean Square Propagation)(済)
AdaDelta(済)
Adam(Adaptive Moment Estimation)(済)

というわけで当初の予定は説明終了。

各最適化アルゴリズムの依存関係

各種最適化アルゴリズムの説明は終わったから
恒例のプログラム化になるのだが、
その前に、これまでの最適化アルゴリズムの依存関係を見てみる。
(何かの拡張がどれとか、あれとそれがくっついてこれになったとかあったので・・・。）

図で示すとこんな感じになる。
括弧内の数値は登場した年とか活躍していいた期間を表している。

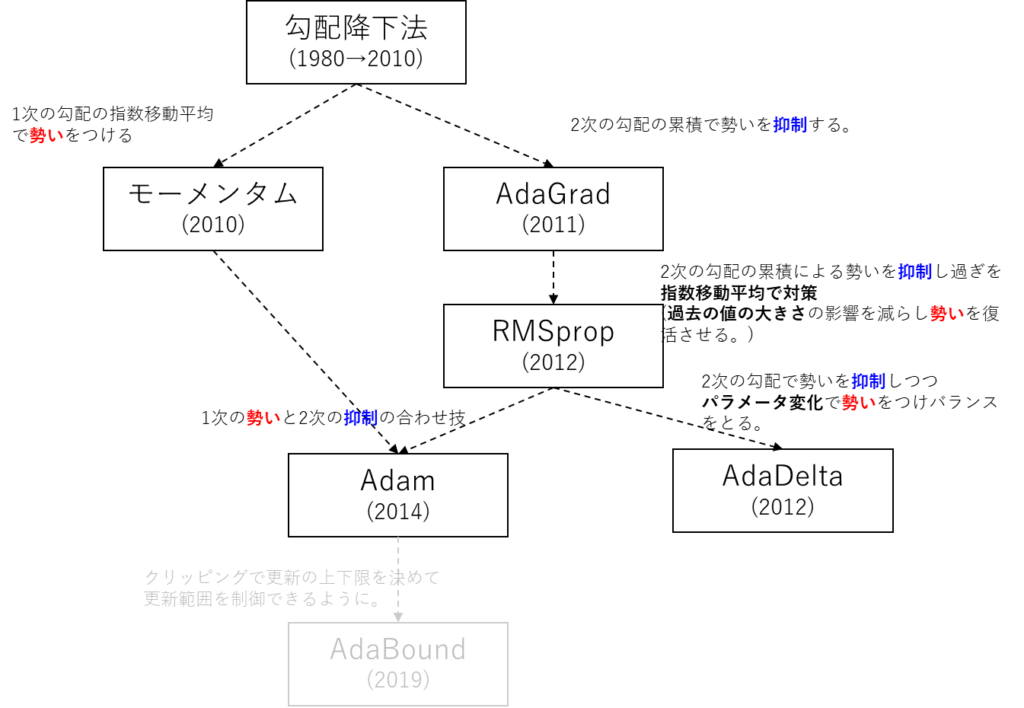
各最適化アルゴリズムの依存関係、勾配降下法(1980→2010)、モーメンタム(2010)、AdaGrad(2011)、RMSprop(2012)、AdaDelta(2012)、Adam(2014)、1次の勾配の指数移動平均で勢いをつける、2次の勾配の累積で勢いを抑制する。2次の勾配の累積による勢いを抑制し過ぎを指数移動平均で対策(過去の値の大きさの影響を減らし勢いを復活させる。)、2次の勾配で勢いを抑制しつつパラメータ変化で勢いをつけバランスをとる。1次の勢いと2次の抑制の合わせ技

全体を見渡せると分かり易い気がしてくる。

基本的には1次の勾配で勢いをつけて、2次の勾配で抑制って感じになる。
その両方を取り込んだのがAdamってことになる。

Adamのあとも、うっすらとAdaBoundっての記載している。
今回は取り扱わなかったが、AdaBoundはAdamの拡張系の最適化アルゴリズム。
差分としてはクリッピングで学習率の範囲を指定できる点。
Adamでも学習率が下がりすぎて更新が効かなくなるのをクリッピングで更新し続けられるような仕掛けが追加されてる。

Adamの更新式【再掲】

ここで各最適化アルゴリズムの説明は終了。
プログラム化に向けての準備をする。

まずはAdamの更新式を再掲しておこう。

\(
\begin{eqnarray}
m_{t+1}&=&\beta_1 m_{t-1}+(1-\beta_1)\nabla J(\theta_t)\\
v_{t+1}&=&\beta_2 v_{t-1}+(1-\beta_2)(\nabla J(\theta_t))^2\\
\displaystyle\hat{m}_{t+1}&=&\frac{m_{t+1}}{1-\beta_1}\\
\displaystyle\hat{v}_{t+1}&=&\frac{v_{t+1}}{1-\beta_2}\\
\displaystyle\theta_{t+1}&=&\theta_t-\frac{\alpha}{\sqrt{\hat{v}_{t+1}}+\epsilon}\\
m_t&:&1次のモーメント\\
v_t&:&2次のモーメント\\
\hat{m}_t,\hat{v}_t&:&バイアス補正項\\
\beta_1,\beta_2&:&指数移動平均係数(\beta_1=0.9,\beta_2=0.999)
\end{eqnarray}
\)