MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 その62【状態空間モデル⑳】
を書き直したもの。
ニュートンの運動方程式を状態空間モデルを離散化したものをC言語でシミュレーションする。
実際にはMATLABコードを元にMATLAB Coderで出力したCコードにちょい修正したものを使用する。
微分解決済みの状態空間モデル
以下がニュートンの運動方程式を状態空間モデルを離散化したもの。
これを(MATLAB経由MATLAB Coder経由の)Cコードで表現する。
状態方程式
\(\boldsymbol{x}(t+\Delta t)=\boldsymbol{x}(t)+\{A\boldsymbol{x}(t)+B\boldsymbol{u}(t)\}\Delta t \)
出力方程式
\(\boldsymbol{y}(t+\Delta T)=C\boldsymbol{x}(t+\Delta t)+D\boldsymbol{x}(t)\)
Cコード
以下がMATLAB Coderが出力したもののちょい修正を入れたもの。
/*
* main.c
*
* Code generation for function 'main'
*
*/
/* Include files */
#include <stdio.h>
#include "rt_nonfinite.h"
#include "main.h"
/* Type Definitions */
/* Named Constants */
/* Variable Declarations */
/* Variable Definitions */
/* Function Declarations */
static void b_statespacemodel(const real_T A[4], const real_T B[2], const real_T
C[4], const real_T D[2], real_T u, real_T dt, real_T x[2], real_T y[2]);
static void eml_xgemm(const real_T A[4], const real_T B[2], real_T C[2]);
/* Function Definitions */
static void eml_xgemm(const real_T A[4], const real_T B[2], real_T C[2])
{
int32_T i1;
int32_T i2;
for (i1 = 0; i1 < 2; i1++) {
C[i1] = 0.0;
for (i2 = 0; i2 < 2; i2++) {
C[i1] += A[i1 + (i2 << 1)] * B[i2];
}
}
}
real_T y[20000];
void main()
{
statespacemodel_motion_raw(y);
}
void statespacemodel(const real_T A[4], const real_T B[2], const real_T C[4],
const real_T D[2], real_T u, real_T dt, real_T x[2], real_T
y[2])
{
real_T dv5[2];
int32_T i;
/* 様態方程式 */
for (i = 0; i < 2; i++) {
dv5[i] = 0.0;
}
eml_xgemm(A, x, dv5);
for (i = 0; i < 2; i++) {
x[i] += (dv5[i] + B[i] * u) * dt;
}
/* 出力方程式 */
for (i = 0; i < 2; i++) {
y[i] = 0.0;
}
eml_xgemm(C, x, y);
for (i = 0; i < 2; i++) {
y[i] += D[i] * u;
}
}
int8_T u[10000];
void statespacemodel_motion_raw()
{
real_T x[2];
int32_T i;
real_T dv0[2];
real_T dv1[2];
int32_T i0;
static const real_T dv2[4] = { 1.0, 0.0, 0.0, 1.0 };
static const real_T dv3[4] = { 0.0, 1.0, 0.0, 0.0 };
/* 時間(横)軸 */
memset(&u[0], 0, 10000U * sizeof(int8_T));
/* 入力信号生成 */
memset(&u[4999], 1, 5001U * sizeof(int8_T));
/* 5秒後に0から1へ */
memset(&y[0], 0, 20000U * sizeof(real_T));
for (i = 0; i < 2; i++) {
x[i] = 0.0;
}
printf("F,v,s\n");
for (i = 0; i < 10000; i++) {
for (i0 = 0; i0 < 2; i0++) {
dv0[i0] = 1.0 - (real_T)i0;
dv1[i0] = 0.0;
}
statespacemodel(dv3, dv0, dv2, dv1, (real_T)u[i], 0.001, x, *(real_T (*)[2])
&y[i << 1]);
printf("%d,%lf,%lf\n",u[i], x[0], x[1]);
}
}
/* End of code generation (main.c) */
ちなみに修正箇所は以下。
ローカル変数に巨大な配列が定義されてしまうので、
それをグローバル変数に移動させた。
以下が該当する。
real_T y[20000];
int8_T u[10000];あとは挙動を確認できるようにprintfを追加した。
シミュレーション結果
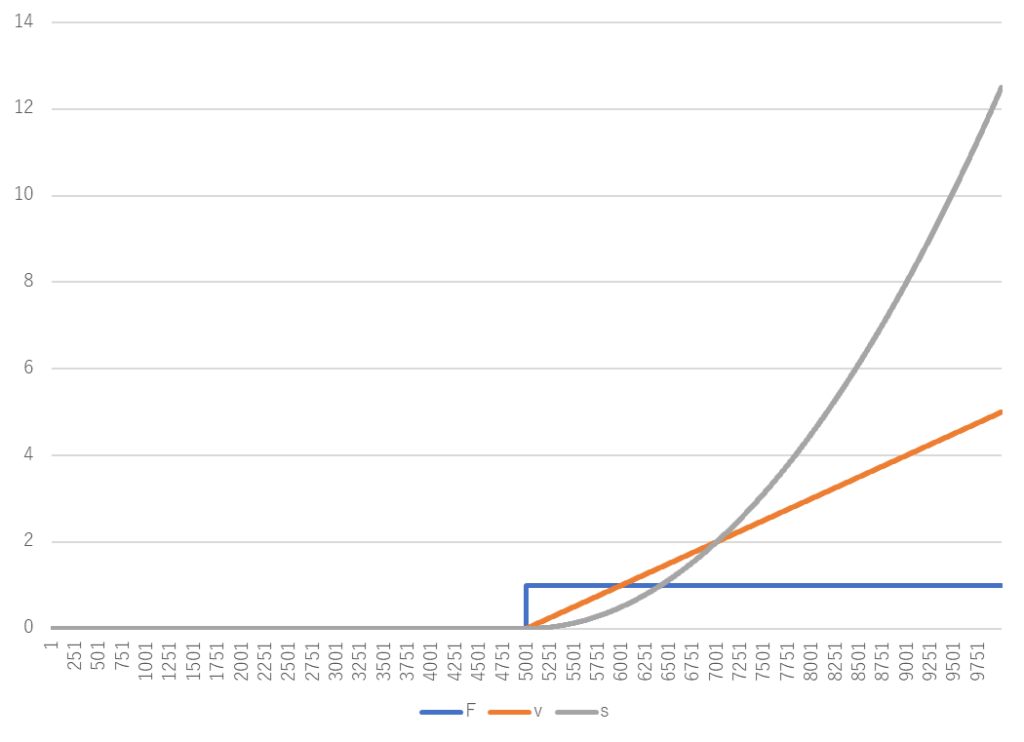
MATLABで挙動確認済みなので当然と言えば当然だが、問題無く動作。
まとめ
- Cコードによるベクトル、行列演算による状態空間モデルの演算実施。
- MATLAB Coderで出力。
- シミュレーション結果も想定通り。
- コード自体は複雑になるが、多変量の微分方程式になった際に効果は大きくなる。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント