掃き出し法(逆行列の求め方)
先の計算では「2×2行列の逆行列の公式」を使用して逆行列を求めたが、
実際には掃き出し法という手法で求める。
掃き出し法は、
\(I\)を単位行列
\(AX=I\)
とした場合、
\(X\)は\(A\)の逆行列である。
という理屈を利用した手法となる。
先の行列に対して、掃き出しを使用して逆行列を求めると以下になる。
\(
A=
\begin{bmatrix}
2 & 3 \\
5 & 1
\end{bmatrix}
\)
↓
\(
\begin{array}{cc|cc}
2 & 3 & 1 & 0 \\
5 & 1 & 0 & 1
\end{array}
\)
2行目に2/5を掛ける
\(
\begin{array}{cc|cc}
2 & 3 & 1 & 0 \\
2 & 2/5 & 0 & 2/5
\end{array}
\)
2行目から1行目を引く
\(
\begin{array}{cc|cc}
2 & 3 & 1 & 0 \\
0 & -13/5 & -1 & 2/5
\end{array}
\)
2行目に5を掛ける
\(
\begin{array}{cc|cc}
2 & 3 & 1 & 0 \\
0 & -13 & -5 & 2
\end{array}
\)
2行目に-3/13を掛ける
\(
\begin{array}{cc|cc}
2 & 3 & 1 & 0 \\
0 & 3 & 15/13 & -6/13
\end{array}
\)
1行目から2行目を引く
\(
\begin{array}{cc|cc}
2 & 0 & -2/13 & 6/13 \\
0 & 3 & 15/13 & -6/13
\end{array}
\)
1行目を2で割り、2行目を3で割る。
\(
\begin{array}{cc|cc}
1 & 0 & -1/13 & 3/13 \\
0 & 1 & 5/13 & -2/13
\end{array}
\)
よって、\(A\)の逆行列\(A^{^-1}\)は
\(
\displaystyle\frac{1}{13}
\begin{bmatrix}
-1 & 3 \\
5 & -2
\end{bmatrix}=
\displaystyle-\frac{1}{13}
\begin{bmatrix}
1 & -3 \\
-5 & 2
\end{bmatrix}
\)
これにより逆行列が求まる。
基本的な演算の流れは、
行列の対角部以外を0になるようにし、
最後に対角部の値で行全体を割って、単位行列にすることで、
元々単位行列側の行列へ掃き出されたものが逆行列となる。
MATLAB等の数値計算ツールや行列を扱える言語に於いては、
逆行列を算出してくれる機能は搭載されているため
実際に自身で掃き出し法を使って逆行列を求めるシーンは少ない。
そもそも連立方程式は何を解いているのか?
連立方程式は、複数の関数の交点を求めている。
以下の連立方程式を元に説明する。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 7 \\
x – y = -1
\end{array}
\right.
\end{eqnarray}
\)
座標を使用して交点を求めると以下。
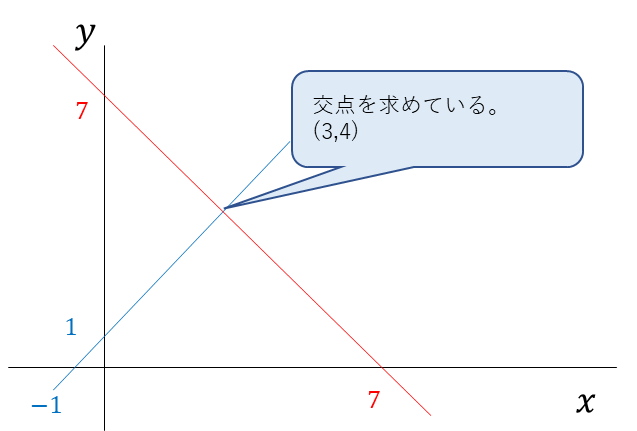
MATLABを使用して解くと以下。
>> inv([1 1;1 -1])*[7;-1]
ans =
3
4このように簡単に交点が求まる。
連立方程式の存在意義は?
連立方程式の使用例:
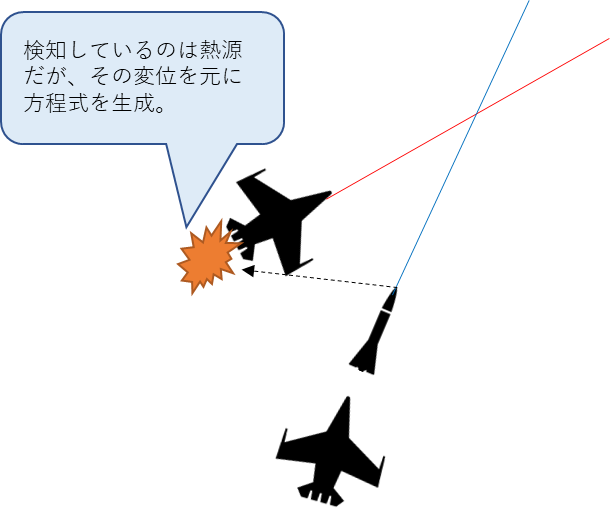
- 戦闘機にミサイルを命中さえるのは、交点を知っている必要がある。
- 自動運転で、自車以外の移動体の予測した上で交点を求めないと衝突回避できない。
などなど。
まとめ
- 簡単に行列の存在意義を説明。
- 当然、連立方程式以外にも利用シーンは多数あるが、まずはシンプルなもので。
- 逆行列は掃き出し法で求められる。
- ただし、ツール、言語側で逆行列を求めれる機能が入っていることが多いので自身で計算することは少ない。
- 連立方程式は複数の関数の交点を求めている。
MATLAB、Python、Scilab、Juia比較ページはこちら
社会のなかの数理 [新装版]──行列とベクトル入門──
なっとくする演習 行列・ベクトル なっとくする演習・行列 ベクトル (なっとくシリーズ)
ゼロからはじめるPID制御
基礎からわかる時系列分析―Rで実践するカルマンフィルタ・MCMC・粒子フィルタ― Data Science Library
観測と最小二乗法―測量・G空間データの解析
ディジタル画像処理[改訂第二版]
高校数学でわかるフーリエ変換―フーリエ級数からラプラス変換まで (ブルーバックス)
マンガでわかるフーリエ解析
入門信号処理のための数学―離散フーリエ変換・離散コサイン変換
はじめて学ぶディジタル・フィルタと高速フ-リエ変換: 基礎・原理からよく理解するための (ディジタル信号処理シリーズ)




コメント