斜面の方向パターン
とりあえず、x方向とy方向のエッジから勾配の方向は特定できそうってところまでやった。
これで、360°どの方向の輝度勾配か特定可能になったと言える。
が、
画像データはピクセルの塊である。
実際、360°で評価することはできるのだろうか?
少なくとも縦と横は判定できそう。
加えて斜めもなんとか可能な感じはする。
斜面の方向パターンを図解
結論を言うと、
評価する勾配方向は
垂直(UD)、水平(LR)、斜め右上から右下(RULD)、斜め左上から右下(LURD)
の4パターンとなる。
勾配方向の角度をこの4パターンに丸める。
67.5[deg]~ 112.5[deg] or -112.5[deg]~ -67.5[deg]だったら垂直。
みたいな感じ。
とりあえず図解しておこう。
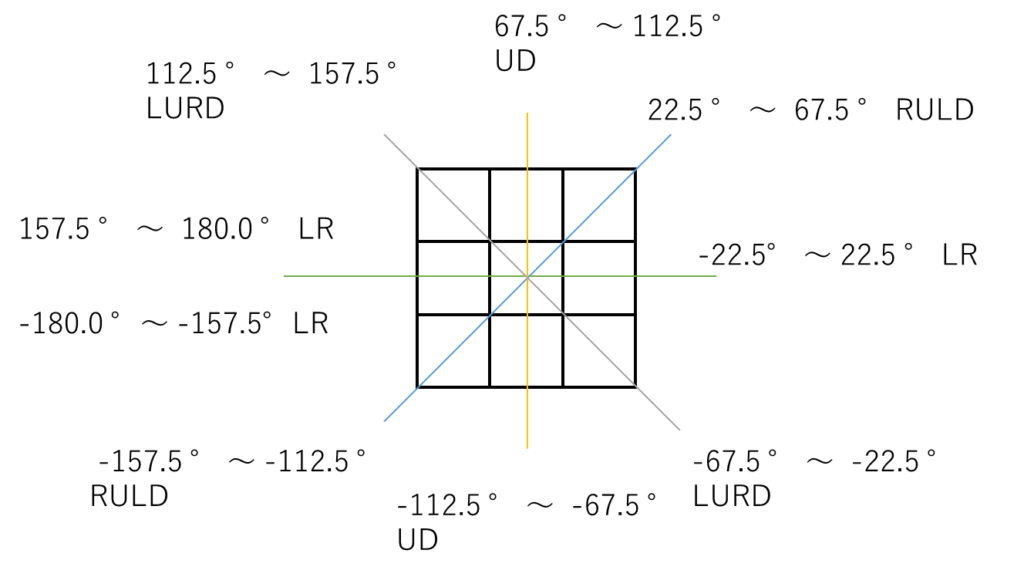
ぱっと見、8方向ではあるのだが、
極大値を判定する際は、逆から見ても評価の線としては一緒なので、
その部分をまとめると4方向になる。
LR:水平
RULD:右上から左下
UD:垂直
LURD:左上から左下
角度を元にした変換表を書くとこんな感じになる。
| 角度[°] | パターン |
|---|---|
| -22.5 ~ 22.5 | LR ─ |
| 22.5 ~ 67.5 | RULD / |
| 67.5 ~ 112.5 | UD │ |
| 112.5 ~ 157.5 | LURD \ |
| 157.5 ~ 180.0 | LR ─ |
| -180.0 ~ -157.5 | LR ─ |
| -157.5 ~ -112.5 | RULD / |
| -112.5 ~ -67.5 | UD │ |
| -67.5 ~ -22.5 | LURD \ |
つまり、中途半端な角度が出ても、この4にパターンに丸めるってことになる。
これは判定するピクセルを3×3マスをベースに考えた場合で、
5×5マス、7×7マスで見て、もっと細かいパターンを出すこともあるらしい。
ここでは3×3マスをベースとした方向の丸めを採用する。
今後の予定
非極大値抑制の理屈的な話は以上になる。
となると、あとは実際にどう試すか。
というところになる。
動作確認用の処理は以下の流れを想定している。
- Sobelフィルタ等の微分フィルタで以下を推定
- x軸、y軸の濃淡変化量
- 変化強度(ノルム)
- 「x軸、y軸の濃淡変化量」から勾配方向角を推定
- arntan関数を利用
- 勾配方向を垂直(UD)、水平(LR)、斜め右上から右下(RULD)、斜め左上から右下の4パターンに丸め。
- 勾配方向角に応じて極大値評価をして非極大値だったら「変化強度(ノルム)」 を0値埋め
- 画像出力
一個一個はこれまでに説明した通りでそれほど複雑ではない。
勾配方向角度について
あと、勾配方向の角度についてだが、一般的には弧度法を使用する。
しかし、今回はイメージのしやすさ重視で度数法を使用する。
弧度法についてはここ参照。
2πが360°、πで180°、1/2πで90°という関係性のもの。
度数法の方がきっと直感的。
というわけで次回から実際にプログラムを組んでいく。
まとめ
- 非極大値抑制(Non-maximum suppression)について説明。
- 概念としてはシンプルだが、2次元平面で考える場合、どの方向から極大値を評価するが重要。
- x方向、y方向の輝度勾配が分かっているので、勾配の方向はarctanで特定可能。
MATLAB、Python、Scilab、Julia比較ページはこちら
社会のなかの数理 [新装版]──行列とベクトル入門──
なっとくする演習 行列・ベクトル なっとくする演習・行列 ベクトル (なっとくシリーズ)
ゼロからはじめるPID制御
基礎からわかる時系列分析―Rで実践するカルマンフィルタ・MCMC・粒子フィルタ― Data Science Library
観測と最小二乗法―測量・G空間データの解析
ディジタル画像処理[改訂第二版]
高校数学でわかるフーリエ変換―フーリエ級数からラプラス変換まで (ブルーバックス)
マンガでわかるフーリエ解析
入門信号処理のための数学―離散フーリエ変換・離散コサイン変換
はじめて学ぶディジタル・フィルタと高速フ-リエ変換: 基礎・原理からよく理解するための (ディジタル信号処理シリーズ)





コメント