【入門】非極大値抑制【数値計算】

勾配の特定方法

いろんな方向から極大値を見つける必要があり、
特に方向を決定するのが面倒そう。

しかし、
実は、Sobelフィルタの時にこれを実現し得る情報をすでに得ている。

Sobelフィルタって横方向と縦方向のエッジ検出を合成したが、
その時に横方向ことx軸、縦方向ことy軸のエッジを得ている。
これらは、各方向の濃淡であり、これを利用すると濃淡の斜面の方向が分かるようになる。

何を言ってるかわからないかもしれないが、
もう少し具体的な話をすると・・・。

x方向が1で、yが0なら横方向の斜面。
x方向が0で、yが1なら縦方向の斜面。
x方向が1で、yが1なら斜め方向の斜面。

実際は切りの良い数値にはならなから、もっと細かい、360°のどこの方向を向いている斜面かが特定可能。
そして、それを角度に表現しなおせば、どの方向の斜面に対して極大値を評価すれば良いかが確定する。

問題はどのように角度にするか。
これは、arctan関数を使えば一撃。

「arctan関数」という名称を見て逃げ出したくなる人もいるかもしれない、
もうちょっと頑張って読み進めて欲しい。
すごく便利な関数なので。

arctan関数はtan関数の逆関数。
tan関数は直角三角形の縦÷横をした結果。
厳密にいうと、
「角度θが分かっていれば、縦÷横の結果を算出できるもの」
になる。

そして、arctan関数は、それの逆のことをしてくれる。
つまり、「縦÷横」が分かっていれば、角度θが求められる。

まず、濃淡のx,yと濃淡斜面方向角度の関係を図示すると以下になる。

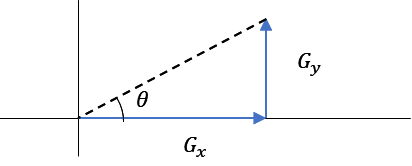
そして、これをtan関数を使って表現すると以下になる。

\(
\displaystyle\tan(\theta)=\frac{G_y}{G_x}
\)

これはtan関数の定義そのものなので問題無いだろう。

これをtan関数の逆関数である、arctanで表現しなおす。

\(
\displaystyle\theta=\tan^{-1}\frac{G_y}{G_x}=\arctan\frac{G_y}{G_x}
\)

どうだろうか？
arctan関数が便利関数であることが伝わっただろうか？

この便利関数を利用すれば一撃で濃淡の勾配方向角度が求められる。