非線形分類を実現
非線形分類を実現方法だが、多層パーセプトロンを使用する。
名前的には単純パーセプトロンを複数にした感じではあるが、まさにその通り。
「複数にする」という考え方には、並列にするか直列にするかという話があるが、
結論としては両方となる。
多層パーセプトロン
とりあえず、単純パーセプトロンと多層パーセプトロンの構造的な違いを確認しておこう。
(差分を知るのが一番手っ取り早いので。)
まずは単純パーセプトロン
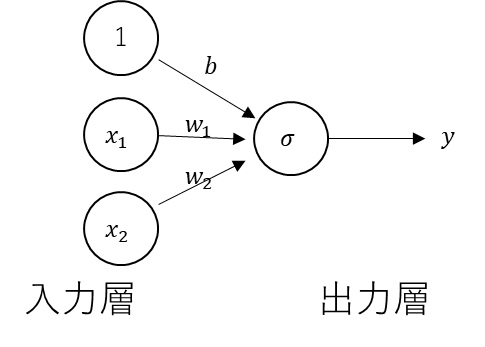
そして、これをベクトル演算で表現するとこんな感じ。
\(
y=\sigma\bigg(
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\1
\end{bmatrix}
\bigg)
\)
活性化関数の話はあるけど、基本的には単なる内積になる。
そして、多層パーセプトロン
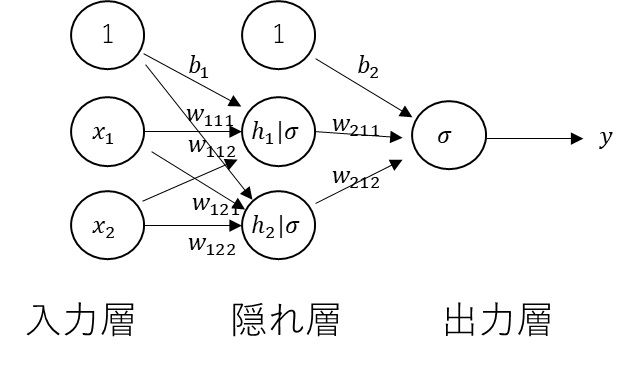
これも行列演算で表現してみよう。
\(
y=
\sigma\Bigg(
\begin{bmatrix}
w_{211}&w_{212}&b_2
\end{bmatrix}
\begin{bmatrix}
\sigma\bigg(
\begin{bmatrix}
w_{111}&w_{112}&b_1\\
w_{121}&w_{122}&b_1
\end{bmatrix}
\bigg)
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}\\
1
\end{bmatrix}
\Bigg)
\)
なんかやべぇことになってる気もするが、ホントにこんな感じ。
ただし、一般的にはこういう数式を書くことは無い。
無理やり書くとこんな感じって程度と思っておいてOK。
ちなみに多層パーセプトロンはニューラルネットワークとも言う。
当然、最も原始的なニューラルネットワークとなる。
まとめ
- 単純パーセプトロンでは分類できないものがある。
- 決定境界直線を求めるというより決定領域を特定するというイメージになる。
- 非線形分類するにはパーセプトロンを複数使う。
- 単純パーセプトロン、多層パーセプトロンの構造と数式を説明。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント