MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その72【非線形分類①】
MATLAB,Python,Scilab,Julia比較 第4章 その73【非線形分類②】
を書き直したもの。
いままでは単純パーセプトロンによる線形分類だった。
今回から、非線形分類に突入。
そして、何を使って非線形分類を実現するかについて。
線形分類から非線形分類
これで、分類はばっちりのような気がするがちょっと待って欲しい。
単純パーセプトロンでも分類できないものがある。
決定境界直線が引けるからだいたい行けそうな気がするが、
この決定境界直線が問題。
単純パーセプトロンは線形分類しかできない。
つまり、線形分類とは別に非線形分類というカテゴリがある。
それに対しては単純パーセプトロンでは実現不可能。
というわけで、単純パーセプトロン以外で実現ってことになる。
まずは、非線形分類がどのようなものなのかを確認していこう。
非線形分類
いままで実施していた分類は線を一本引いて、決定境界を見つけ出す、
線形分類と呼ばれるもの。
しかし、世の中、線形分類だけでは分類できないものが多い。
例えば、論理ゲートのXORなどが代表的。
図で書くと以下になる。
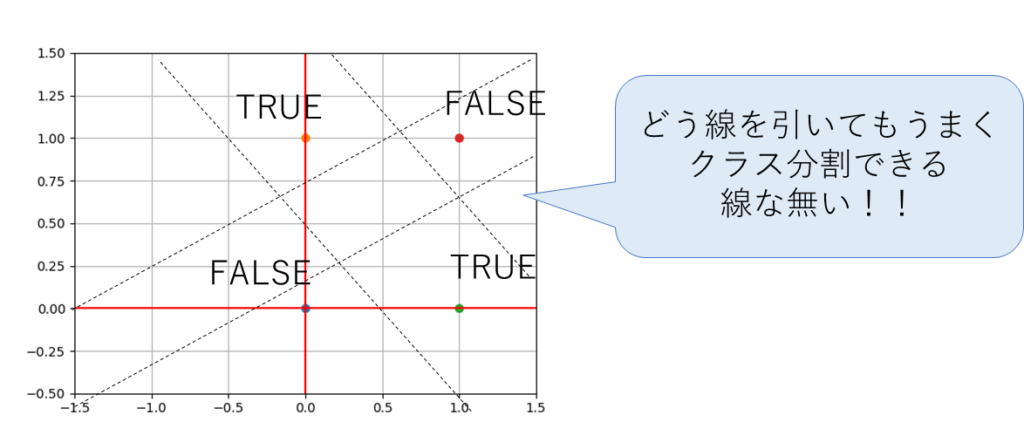
つまり、TRUEとFALSEが対角線上にいるから1本の線では上手くわけられない。
こういうものを「線形分離不可」「非線形分離」と言ったりする。
決定領域
それでは、どういうふうに分類されれば正解って言えるのだろうか?
図にすると以下になる。
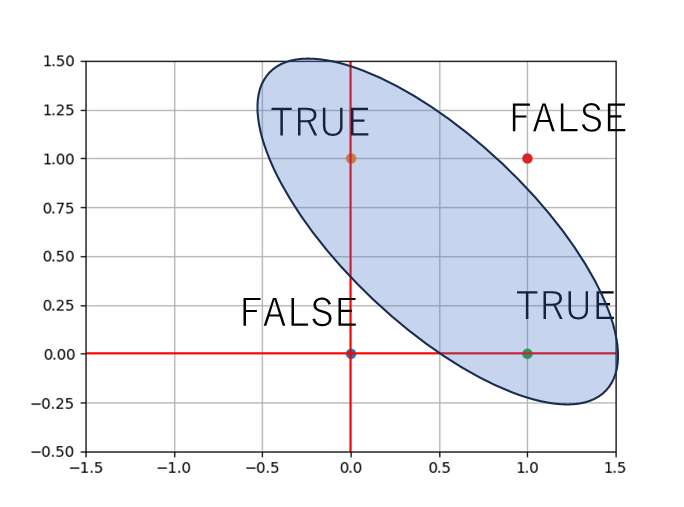
この楕円部分を決定領域と言ったりする。
実際の分類の結果がこのようにキレイな楕円になるとは限らないけ。
あくまで理想的な分類結果としてはこうな感じってところ。
次のページへ
次のページでは、非線形分類を行うための手法について





コメント