【入門】多変量多項式回帰分析(Python)【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
正規方程式、各パラメータ、推定対象の多項式再掲
Pythonコード
処理結果
考察
まとめ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その69【多変量多項式回帰分析③】

を書き直したもの。

正規方程式を用いた、多変量多項式回帰分析について。
今回は、Python(NumPy)で演算してみる。

正規方程式、各パラメータ、推定対象の多項式再掲

正規方程式と多変量多項式回帰分析で想定するパラメータの再掲。

正規方程式

\(
x=(A^TA)^{-1}A^Tb
\)

多項式回帰分析に於ける各パラメータ

\(
A=
\begin{bmatrix}
x_1^2 & x_1y_1 & y_1^2 & y_1 &1\\
x_2^2 & x_2y_2 & y_2^2 & y_2 &1\\
\vdots & \vdots & \vdots\\
x_n^2 & x_ny_n & y_n^2 & y_n &1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma\\
\delta\\
\epsilon\\
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{bmatrix}
\)

推定対象の多項式

\(
z=4x^2-5xy+3y^2+y+2
\)

これをPython(NumPy)で実現する。

Pythonコード

Pythonコードは以下になる。

import numpy as np
import matplotlib.pyplot as plt

n = 100

x = np.random.rand(1, n).reshape(-1,1)
y = np.random.rand(1, n).reshape(-1,1)
z = 4*x**2 - 5*x*y + 3*y**2 + y + 2 + np.random.rand(n, 1) -0.5

A=np.block([x**2, x*y, y**2, y, np.ones((x.size,1))])
b=z
X=np.linalg.inv(A.T@A)@A.T@b
print(X)

fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
ax.scatter3D(x, y ,z)
xp=np.linspace(0, 1, 5)
yp=np.linspace(0, 1, 5)

xpm,ypm=np.meshgrid(xp,yp)
ax.plot_wireframe( xpm, ypm, X[0]*xpm**2 + X[1]*xpm*ypm + X[2]*ypm**2 + X[3]*ypm +X[4])
ax.view_init(elev=20, azim=230)

plt.show()

処理結果

処理結果は以下。

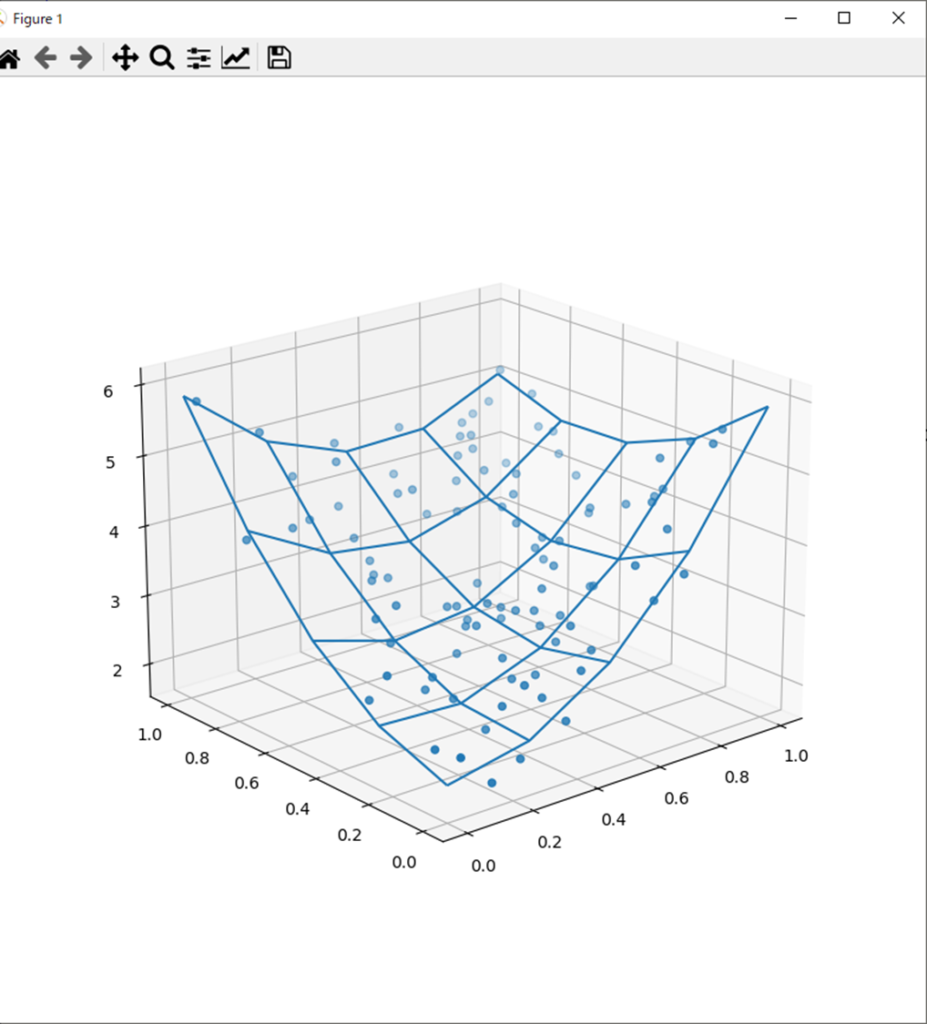
[[ 3.88828397]
 [-4.68917615]
 [ 3.06717692]
 [ 0.74666453]
 [ 2.04172518]]

考察

これも流れとしては一緒。
式が複雑になってきたせいか、少しコードが読みにくくなってきてはいる。

MATLAB等であれば、割と元の式の形状が残るため、あまり気にならない。
対して、Pythonの場合は、式が複雑になると読みにくくなる傾向はある。

NumPyがベクトル、行列の演算をサポートしてるってだけで、
Python自体は一般的なプログラミング言語なわけだから仕方のない面はある。

まとめ

正規方程式による多項式回帰分析をPython(NumPy)で実施。
誤差はあるものの目的の係数の算出はできている。
式が複雑になってくると、Pythonコードだと元の式の表現から乖離しているのがちょっと気になる。

MATLAB、Python、Scilab、Julia比較ページはこちら