バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回まで3回に分けてはテイラー展開を応用した微分、積分の説明をした。
今回をそれをPID制御に適用して離散化する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
速度型PIDの復習

で、今回はPID制御の離散化をするんだよね?

そうだね。
とはいえ、間に3回の離散化説明回を挟んだので、
今回使用する速度型PIDの復習をしておこう。

あ、僕が説明したい!

お、いいね。
知った知識を自分の言葉でアウトプットし直すことは良いことだ。
というよりも、
知識というものはインプットとアウトプットの両方が出来て初めて知識と言っても良い。

なるほど!

よし!
ちゃんとアウトプットして知識にするぞ!

- まずPID制御は位置型PIDと速度型PIDがある。
- 位置型PIDは積分項の影響でワインドアップという問題を抱えている。
- 速度型PIDは位置型PIDを微分してから積分し直したもの。
- 速度型PIDはは積分要素だけが式の外側に出てくる
- この積分要素をコントロールしてワインドアップの問題を解消する。
式にすると以下。
$$u(t) = \int (u(t) \frac{d}{dt})dt$$
$$= \int (K_p e(t) \frac{d}{dt}+ K_i e(t)+K_d e(t) \frac{d^2}{dt^2} )dt$$
絵に描くと以下。
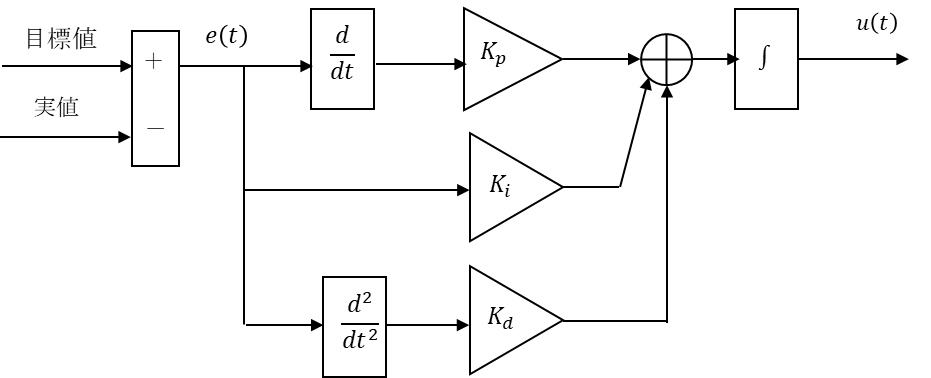

おー。バッチリだ!

で、これを離散化するわけなんだけど、
総和法と差分法で良いのかな?

求められる精度次第ではあるが、
今回は微分積分そのものの精度が必要と言うよりも微分と積分の特性が欲しいだけなので、
総和法、差分法で良いと思うよ。

オッケー
PID制御の離散化

んじゃ、まずは外側にいる積分を総和法に置き換える。
$$u(t)≒Σ(K_p e(t) \frac{d}{dt}+ K_i e(t)+K_d e(t) \frac{d^2}{dt^2} )Δt$$

そして、内側の微分を差分法に置き換える。
$$u(t)≒Σ((K_p \frac{e(t)-e(t-1)}{Δt}+ K_i e(t)+K_d \frac{e(t)-e(t-1)}{Δt} \frac{d}{dt} )Δt)$$
まだ微分が残ってるので、それも差分法で置き換える
$$u(t)≒Σ(K_p \frac{e(t)-e(t-1)}{Δt}+ K_i e(t)+K_d \frac{\frac{e(t)-e(t-1)}{Δt}-\frac{e(t-1)-e(t-2)}{Δt}}{Δt} )Δt$$

こ、これは・・・。
シンプルになると思っていたけど、むしろカオスになった。

まぁ、
微分積分自体がいろんな意味を内包しているからね。
特に時間に関係する情報が表に出てきてしまったんでパラメータが増えるようには見えるね。
無条件にブロック線図に書き直すと以下になるよ。
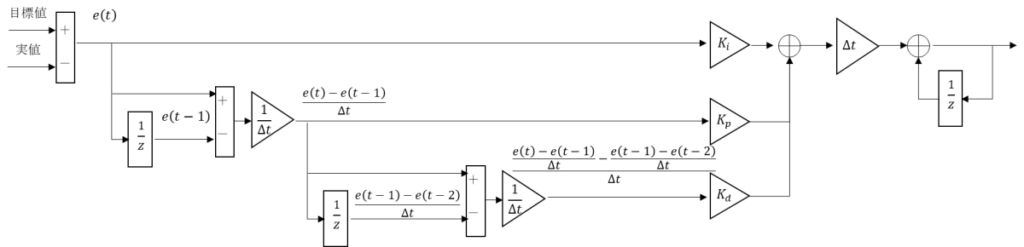

この\(\displaystyle\frac{1}{z}\)ってのは、
前回値ってことでいいんだよね?

そうだね。
z変換したときに出てくるものだけど、
zの指数がサンプルのタイミングを示しているんだ。
\(\displaystyle\frac{1}{z}\)は\(z^{-1}\)ってことなんで、
現在より一つ前のサンプルであることを示す。

前回値ってことでいいんだよね?

・・・。
いいよ。

\(Δt\)はどうなるのかな?

今回の場合だと制御周期ってことになるね。
制御周期はどのくらいを想定しているの?

ECU側が\(10[ms]\)でアクセル開度をサンプリングしているらしいんで、
APコントローラも\(10[ms]\)で駆動するつもりだよ。
ってことは、\(Δt\)は今回の場合は\(10[ms]\)ってことになるね。

そういえば、ワインドアップ対策ってどうなるの?

あー、最終段の積分要素の部分に切り替えSWとサチュレーションを入れれば良いよ。
描くとこんなん。
![制御開始トリガサチュレーション付きPID制御器、1/Tc、制御周期[sec]、目標値、実値](https://www.simulationroom999.com/blog/wp-content/uploads/2020/06/03_離散化PIDワインドアップ抑制-1024x350.png)

おー!
これだと、変に積分要素で値が大きくなることもないし、
自動制御前の出力を継承できるから、自動制御に移っても出力が暴れないね。

ん?
ここまで来ると・・・。
このままSimulinkで記載できそうな?

できるね

お。
と言うことは早々にシミュレーション可能?

うーん、
動くには動くけど、
制御対象が居ないんで正常かどうかってシミュレーションはできないかな。

あー。
確かに。

というわけで、
次回は制御対象側かな。
まとめ

まとめだよ。
- 速度型PIDの復習。
- PIDの積分を総和法で、微分を差分法に置き換えた。
- \(Δt\)は制御周期。
今回の場合は\(10[ms]\)。
・ワインドアップ対策は積分要素に切り替えスイッチとサチュレーションを含めることで対応。
バックナンバーはこちら




コメント