バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回、簡易HILS案の関係者間調整と物理値変換仕様を実施。
今回は実際の制御モデルに踏み込む。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
位置型PID制御

前回は「足回り」をやったから、
今回は制御の部分になるのかな?

そーだね。
どういう制御をイメージしているの?

やっぱり、
基本のPID制御を組み込むのが良いと思うんだよね。
ただ、
実はすでに組み込まれているPID制御の調整はしたことあるんだけど、自分で仕様書書くとなるとどうしたら良いのやら・・・。

じゃあ、
まず簡単に普通のPID制御から話すか。

普通の?
普通じゃないPID制御があるの?

最初の話すのが「位置型PID」と呼ばれえるもので、
PID制御を定義する式をそのまま使ったもの。
これの欠点を話して、
次に「速度型PID」と呼ばれるものを説明するつもりだ。

察すると、
「位置型PID」は何か問題があるから
「速度型PID」の方がいいよってことかな?

そういうこと。

まずPID制御を定義している式は以下になる。
$$u(t)= K_p e(t)+ K_i \int e(t) dt +K_d e(t) \frac{d}{dt}$$

各ゲインの\(K_p\)、\(K_i\)、\(K_d\)を調整すれば、
様々な制御対象に適用できるってのが利点なんだよね。

そうそう。
ブロック線図で書くと以下になる。
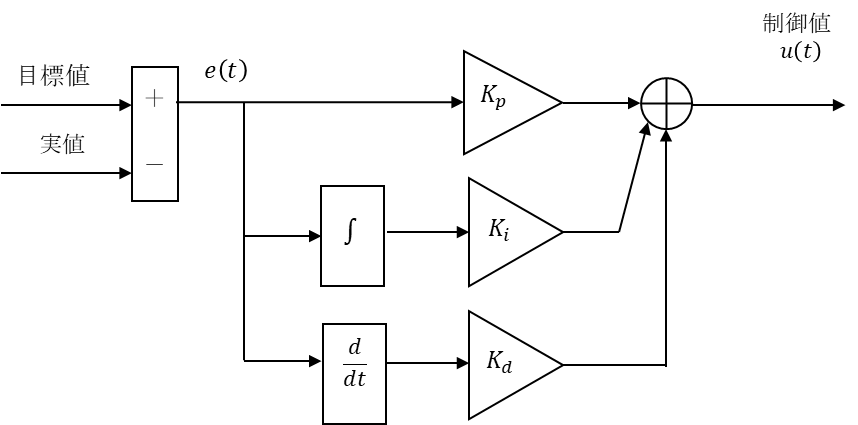

で、これに問題があると。

うん。今回の場合は特に。

というと。

今回の仕様だと、
人間がアクセルを踏んである程度の速度が出ている状態から、
自動制御に移るんじゃない?

そうそう。
使用感は調整になると思うけど、
目標値より\(20[km/h]\)引いたあたりから自動制御になる感じ。

とすると、
やはりワインドアップという現象に悩まされることになる。

ワインドアップ?
何それ?

PID制御は目標値と現在の差を無くすような出力をするんだけど、
差が中々縮まらないようだと
積分項が差を埋める方向に値をため込むんだ。
例を出すと以下のような動きになる。
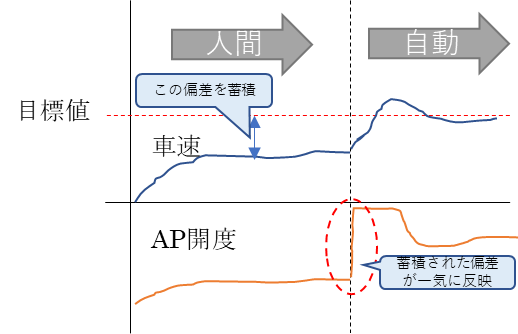

って、
ことは自動制御に移った瞬間に
一気にアクセルを踏むような動作で危ない!!

でも、だったら、
自動制御に移るまではPID制御は動作しないようにしておけば
積分項が値をため込むことは無いんじゃない?

それだと今度は、0値からの制御になるので、アクセル開度が一旦0近傍まで落ち込むという不安定さが出るね。
こんな感じかな。
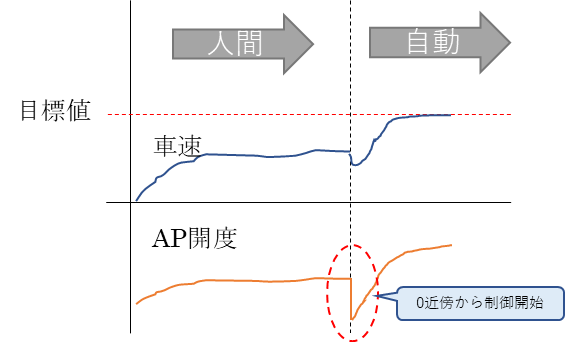

あ、そうなるのか。
これが位置型PIDの欠点ってやつなのか。

でも、
速度型PIDだとここら辺は解消されるんだよね?

そうなるね。
速度型PID制御

で、
速度型PIDってのは何?

一言で言うと、
「位置型PIDを微分して積分したもの」
になる。

え?

式で書くとこうだ。
$$u(t) = \int (u(t) \frac{d}{dt})dt$$
$$= \int (K_p e(t) \frac{d}{dt}+ K_i e(t)+K_d e(t) \frac{d^2}{dt^2} )dt$$

そして、ブロック線図で書くとこうなる。
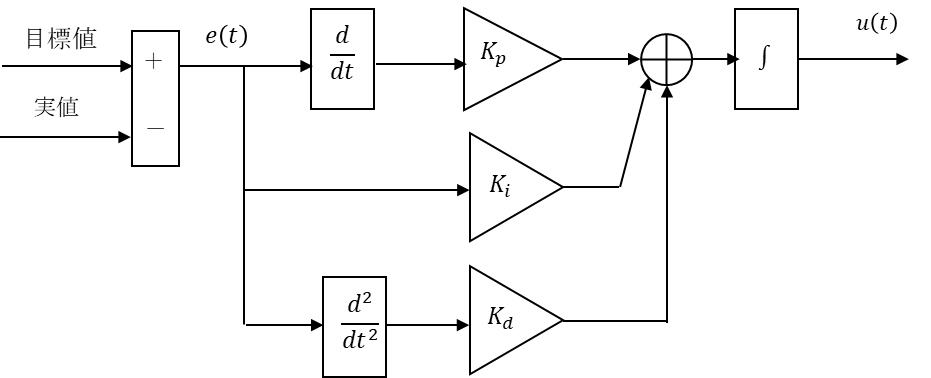

(なんか2階微分が居る・・・)

えーっと、
微分して積分すると元に戻っちゃうんじゃないの?

厳密には元には戻らない。
微分した時に、バイアスが消える。
積分した際に積分定数がバイアス相当。
やりたいことは、過去のバイアスを消して、現在値を初期条件として再定義するところにある。

ごめん。良く分からない。

言い換えると、問題になっている積分項を外側に追い出して、
その積分項を自動制御するタイミングの現在値で上書きするイメージかな?

イマイチぴんときてないけど、
問題の積分項をコントロールしやすいところに配置し直して、都合の良い初期値を設定できるようにしたってことかな?

そうなるね。
具体的なイメージは離散化したブロック線図にすると分かるかもしれない。

離散化?

うん。
ソフトウェアで実現しようと思ったら、
今の形だとできないんで離散化が必要。

えーっと、
それも解説してくれるんだよね?

じゃ、
次回のネタはそれにするか。
まとめ

まとめだよ。
- PID制御は位置型と速度型がある。
- 位置型はワインドアップの課題を抱えている。
- 速度型はワインドアップの課題を解消しており、使い勝手が良い。
- ソフトウェアで実現するには離散化が必要。
バックナンバーはこちら




コメント