バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回のプラントモデルの精度向上の続き。
今回は実際にモデルの修正までする。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
振り返りと方針

さて、
前回プラントモデルをよりリアルにしたわけなのだけど。

そこで出てきた問題として、
制御が振動するようになってしまったんだよね。

そうそう。

んで、
PIDの各係数を調整すれば良いかと思ってたんだけど、
フクさんとしては別の手段があるような言い方してたよね?
どんな感じなの?

一言でいうと、
「積分単位時間を調整する」

????
積分単位時間

ちょっと例題を出そう。
以下の積分するといくつ?
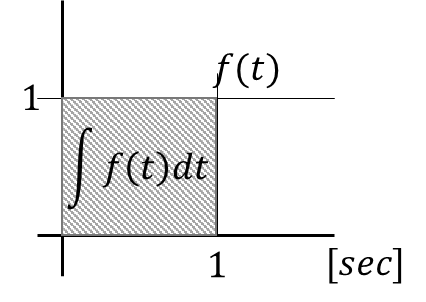

縦軸1で横軸1だから
これは積分するまでもなく、答えは\(1\)だ!

正解。

では、
似たような感じだけどこれは?
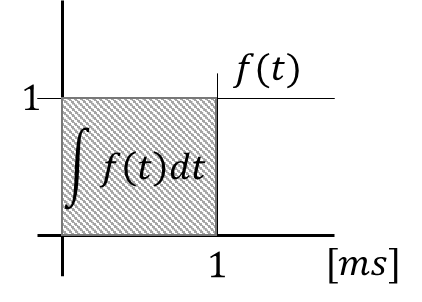

あれ?
えっと、これも・・・1かな?

正解。

え?正解なの?
不正解の流れだと思ってた。

じゃこれは?
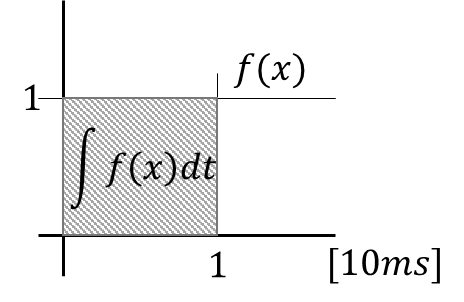

・・・。
これも・・・(ゴクリ)・・・い、1?

正解。

何となく分かってきたぞ。
ようは横軸の単位をどう取るかで同じ1でも積分の意味が変ってくるってことだね?

その通り。
PIDモデル修正

この考え方をPID制御モデルに取り込むと以下のようになる。
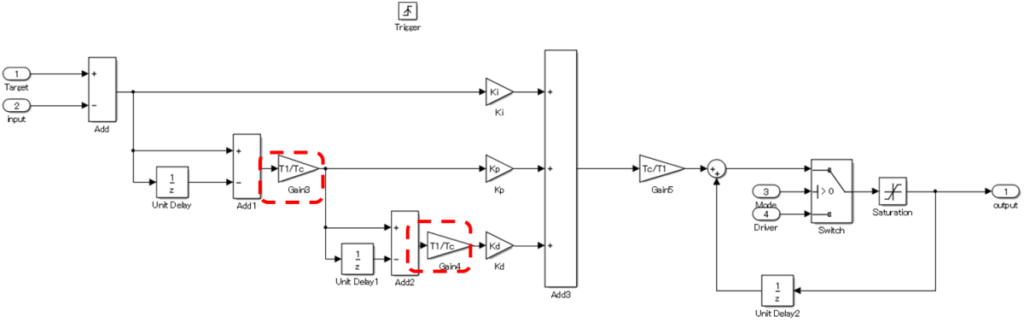

\(Δt\)の分母側と\(\displaystyle\frac{1}{Δt}\)の分子側に\(T1\)ってのが付いたね。

これは\(Δt\)の単位を意味する。
いままでは\(1[sec]\)想定の計算だったんで\(1\)という値が居たことになる。

ということは今回はこれを調整するってことになるのかな?

そうだね。
積分単位時間の調整

で、調整といってもどういうふうに調整すれば良いのかな?

一次遅れ系の時定数的なイメージでおおよそOKかな?

じゃー、11.5ってのを入れてみよう。
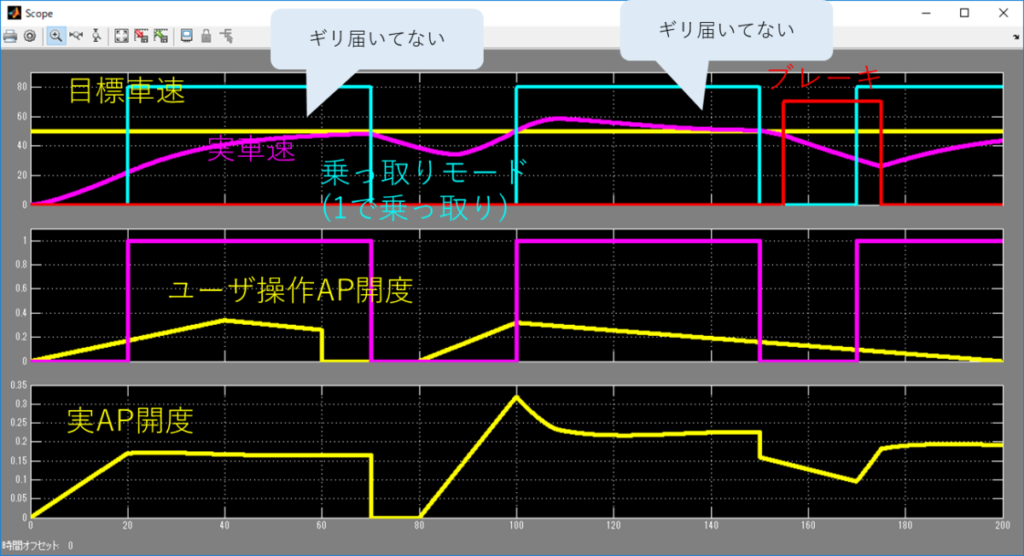

んー、
振動はしなくなった・・・かな?

制御側の積分単位時間\(T1\)をプラント側の時定数と合わせこんだので、振動は無くなった。
しかし、ちょっと反応が鈍い。
少し積分単位時間\(T1\)を下げてみる。

じゃあ、\(T1=5.5\)くらいでやってみるね。
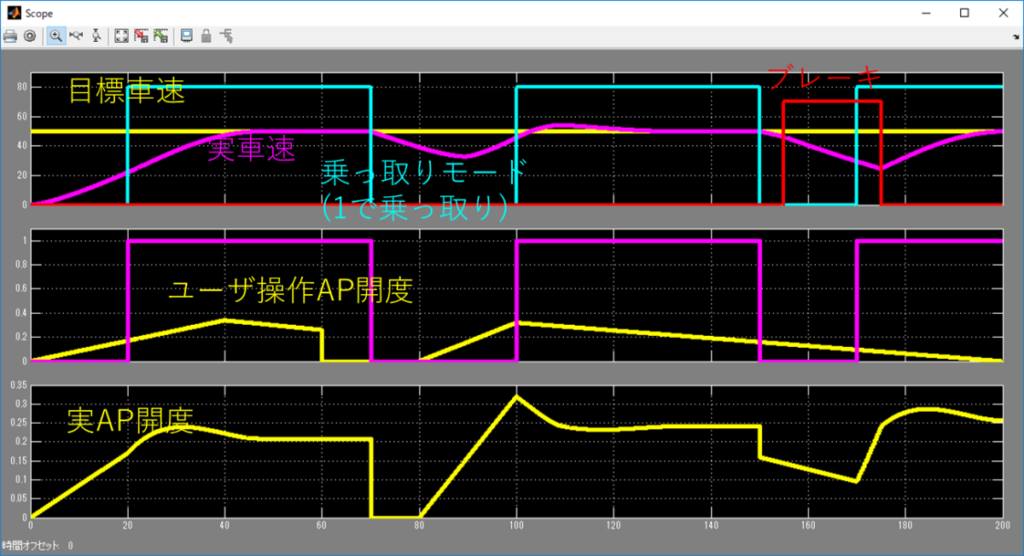

お、今回はいい感じじゃないかな。

振動もせず、そこそこの追従性がある状態になったね。
おおよそ、期待する追従時間の\(30~50[\%]\)くらいの時間を目安として、
積分単位時間T1を設定すると良いのかもね。

うーん、こういう調整の仕方もあるのかー。
普通のPIDでチューニングしたら?

今回のやり方って、
一般的なPIDのチューニングに当てはめるとどういう感じになるのかな?

普通に時間関係の係数をPIDの各係数として計算すると出てくるよ。
こんな感じだね。
| \([K_p, K_i, K_d]\) | |
| 調整前(積分単位時間T1=1) | \([0.80000, 0.00500, 0.00100]\) |
| 積分単位時間T1=5.5 | \([0.80000, 0.00091, 0.00550]\) |
| 積分単位時間T1=11.5 | \([0.80000, 0.00043, 0.01150]\) |

\(K_p\)は変化せずに\(K_i\)と\(K_d\)を調整したような感じになるんだね。

そうなるね。
慣れている人だと振動の仕方から
「積分係数\(K_i\)が強そうだからちょっと落としてみよう。」
みたいな判断になるのかもね。

慣れている人並みのチューニングがサクっとできてしまうのかぁ。

まぁ今回のモデルはシンプルであったのと、時定数を大きく弄った事実をしっていたからね。
何も分からない状態だと慣れている人の方がうまいチューニングはすると思うね。

うん。勉強になったよ。

じゃ、
その勉強ついでに次回もPIDの特殊なパラメータを弄ってみようか。

(まだなんか隠し持ってるのか?!)
まとめ

まとめだよ。
- 時間も調整可能パラメータの一部と考える。
- さらに時間の単位も調整可能のパラメータと考えられる。
バックナンバーはこちら




コメント