バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回のプラントモデルの精度向上の続き。
今回は実際にモデルの修正までする。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
定常ゲインを求める

さて、前回の続きと言うことで
一次遅れ系の定常ゲインを求める。
まずイメージ。
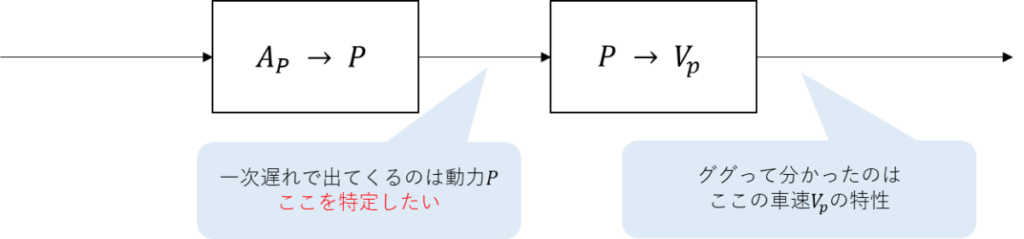

なるほど。
出力から車速までの演算が邪魔ってことなんだね。

その通り。
前回のグラフに対しての同定は車速\(V_p\)に対しての特性なので、
動力\(P\)としての特性を算出する。
こんな感じ。
\(F:\)力\([N]\)
\(P:\)出力(仕事率)\([W]\)
\(v:\)車速\([m/sec]\)
\(a:\)加速度\([m/sec^2]\)
\(m:\)車両重量(質量)\([kg]\)
$$F=ma$$
$$a=\frac{dv}{dt}$$
$$P=Fv=mav=m\frac{dv}{dt}v$$

出力と車速の関係が出たってところかな。

うん。
そして、車両重量を\(1150[kg]\)
アクセル開度MAX時の最高速度を\(200[km/h]\)こと
$$200[km/h]×1000[m/km]÷60[min/h]÷60[sec/min]$$
$$≒55.56[m/sec]$$
平均加速度を
$$(55-10)[km/h]÷31[sec]$$
$$=1.45[km/hsec]$$
$$=1.45[km/hsec]×1000[m/km]÷60[min/h]÷60[sec/min]$$
$$≒0.403[m/sec^2]$$
出力と車速の関係式から
$$K=1150[kg]×55.56[m\sec]*0.403[m/sec^2]$$
$$=25749.282$$
となる。
この\(25749.282\)が定常ゲイン。

うーん、
サクサクとよく計算できるもんだなぁ。

事前に計算して検算もした。
こんなのカンペ無しで言えるわけないだろう。

(やっぱりカンペがあったのか。)
プラントモデルの修正

次にプラントモデルを修正する。

あ、加速時と減速時で時定数を変更するんだよね?
僕がモデルの修正するよ。

じゃー任せた。
~ 10分後 ~

できた!
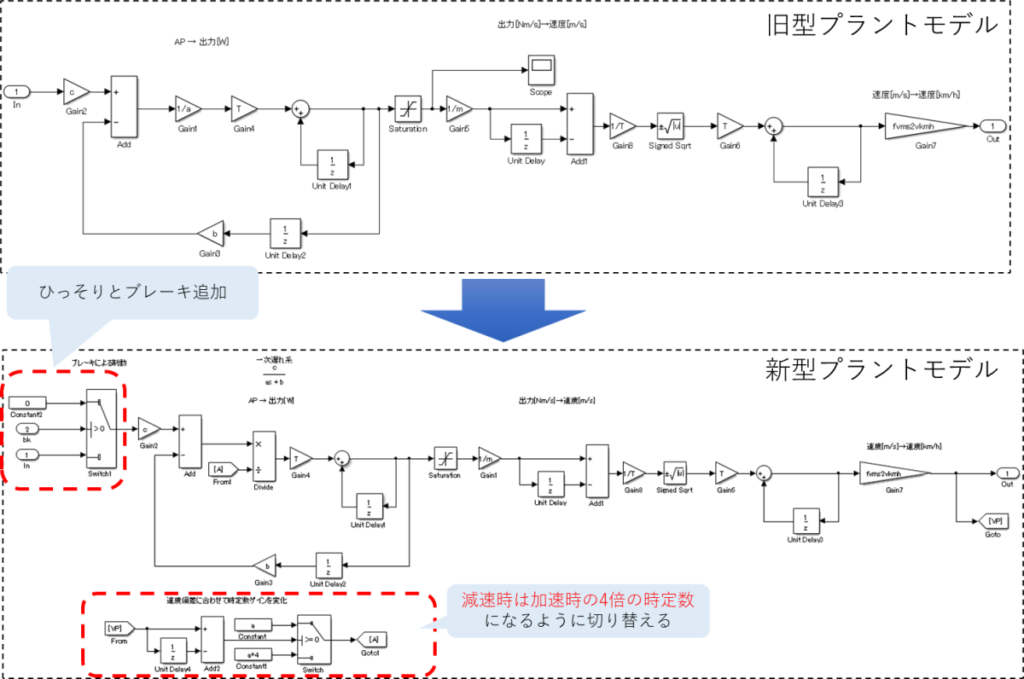

うん。バッチリOKだ。
特に指摘は無いよ。

おー!初めての一発OK!
シミュレーションしてみる

んで、
そのままシミュレーションしてみなよ。

あいよ!

・・・。
あれ?

どうかした?

なんかちょっと制御が振動しちゃってるんだよねぇ。
自動制御に移った段階で一気に踏み込んでる感じで。
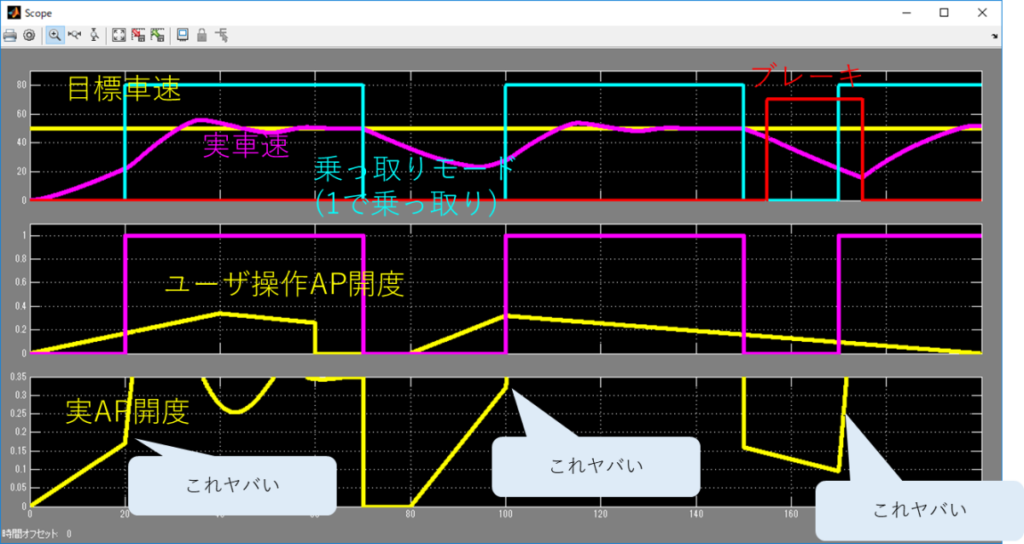

PIDのゲインが強いんだね。

ということは\(K_p\)と\(K_i\)を下げてあげれば良いってことだね。

まぁPID制御としてはそうなるが、
\(K_p\)と\(K_i\)はそのままにしておこう。
次回、別のパラメータを調整することで振動を抑えるのに挑戦してみよう。

制御器も修正がいるのか?!
まとめ

まとめだよ。
- 出力(仕事率)と速度の関係は質量が確定していれば算出可能。
- 最大速度が確定していれば、定常ゲインが算出可能。
バックナンバーはこちら




コメント