バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回で、おおよその仕様決めは終わったと思われた。
しかし、太郎くんのド忘れ発覚によりフィルタ仕様も考える必要が出てきた。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
ノイズとフィルタの種類

んで、
A/Dの入力にフィルタを掛けたいんだけど、
ざっくりどうすればいいんだろうね?

目的によるかな?

目的?

そうそう。
今回の装置はアクセルとECUの間に挟み込むんだけど、
想定されるノイズってどういうのがあるのかなって話。

うーん、ノイズの種類かー。
ちょっとわからないなー

まぁノイズを並べると以下かな。
- サージ
- リプル
- スパイク
- クロストーク
- フリッカノイズ
- ショットノイズ
- ホワイトノイズ

ここら辺はハード担当が何とかしてそうだけど・・・。

ソフトウェアとしては、
スパイクと
ホワイトノイズ
を除去くらいでいいかな?

単純に移動平均とかじゃだめ?

ホワイトノイズはそれで良いが、
スパイクはそれだと抑制は出来ても除去しきれ合いで影響が残るかな。

どうしたら良いの?

一般的には
ホワイトノイズ → 移動平均で除去
スパイク → メディアンフィルタで除去

ということは2種類のフィルタを掛ければ良いってことかな?

それでも良いけど、移動平均とメディアンフィルタの両方を掛けると真値が出るまでに結構な時間(周期)を要するね。

うーん、なんかホワイトノイズとスパイクの双方を除去できる調度良いフィルタってないの?

あるよ。

あるんだったらそれを先に!

シグマフィルタってのがある。

どういうの?

平均値から標準偏差\(σ\)に入ってるデータだけを平均して真値とする。

どういう効能があるの?

移動平均とメディアンフィルタの両方の特性を持ってる感じかな。

じゃー今回必要なフィルタの要件とマッチしているってことだね!
説明よろしく!
シグマフィルタ

ざっと手順を説明するよ。
凡その流れは以下。
①平均値\(μ\)算出
②各要素の平均値\(μ\)との偏差\((x_n-μ)^2\)を算出
③分散\(σ^2\)算出
④標準偏差\(σ\)算出
⑤平均値\(μ\)±標準偏差\(σ\)の範囲内の要素のみ平均値を算出
(これにより外れ値の除去が可能)
ただし、平方根\(sqrt()\)の演算が処理速度への影響が読めないため、
④と⑤の手順を無くし、
かわりに、偏差 \((x_n-μ)^2\)から分散\(σ^2\)を引いた結果として0以上の要素を
平均値\(μ\)±標準偏差\(σ\)の範囲内とする。
絵で描くとこんなイメージ。
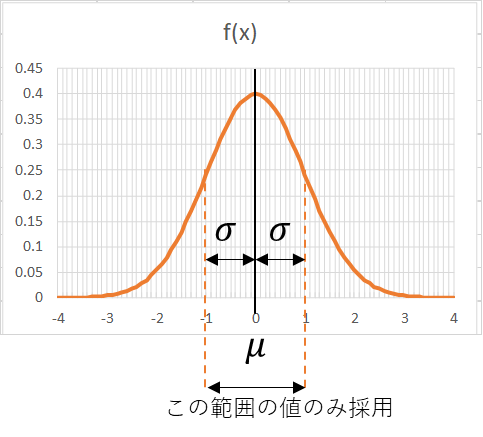

んで、実際の計算はどうするの?

こんなん。
まず、取得したサンプルの平均値\(μ\)を算出。
$$μ=\frac{1}{n}\sum^n_{i=i}x_i$$
平均差二乗数列を算出。
$${a_n}:=({x_n}-μ)^2$$
分散\(σ^2\)を算出。
$$σ^2=\frac{1}{n}\sum^n_{i=1}a_i$$
標準偏差\(σ\)の範囲内の要素を特定する。
$${b_n}:={a_n}-σ^2$$
$${c_n}:=({b_n}≦0)$$
必要な要素だけの平均を求め、それを真値とする。
$$y=\frac{\vec{x_n}・\vec{c_n}}{\displaystyle\sum^n_{i=1}c_i}=\frac{\vec{x_n}\vec{c_n}^T}{\displaystyle\sum^n_{i=1}c_i}$$

えーっと、”\({a_n}:=\)”って何?

数列表現とその代入表現。

“\(\vec{c_n}^T\)”って何?

転置。

ググります!

Simulinkで描くとこんな感じ。
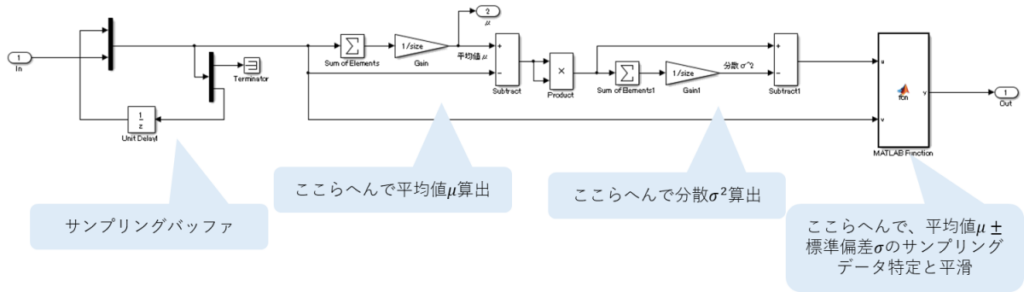

念のため簡単に動作確認してみるか。
こういう入力を入れてみる。
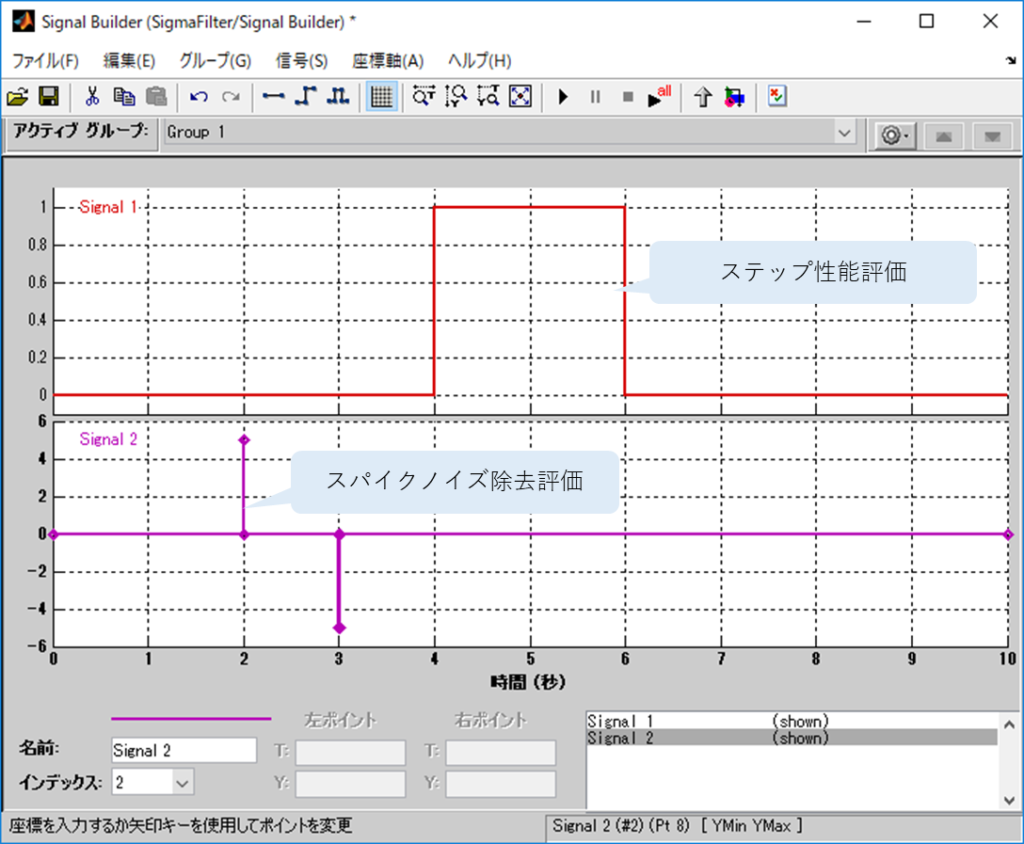

実際には、これにホワイトノイズ相当の信号を合成するけどね。

なるほど。
この飛び出しているのが
疑似的なスパイクノイズだね。

で、実際の入力と出力。
ついでに移動平均だけだとどうなるかも出してみたよ。
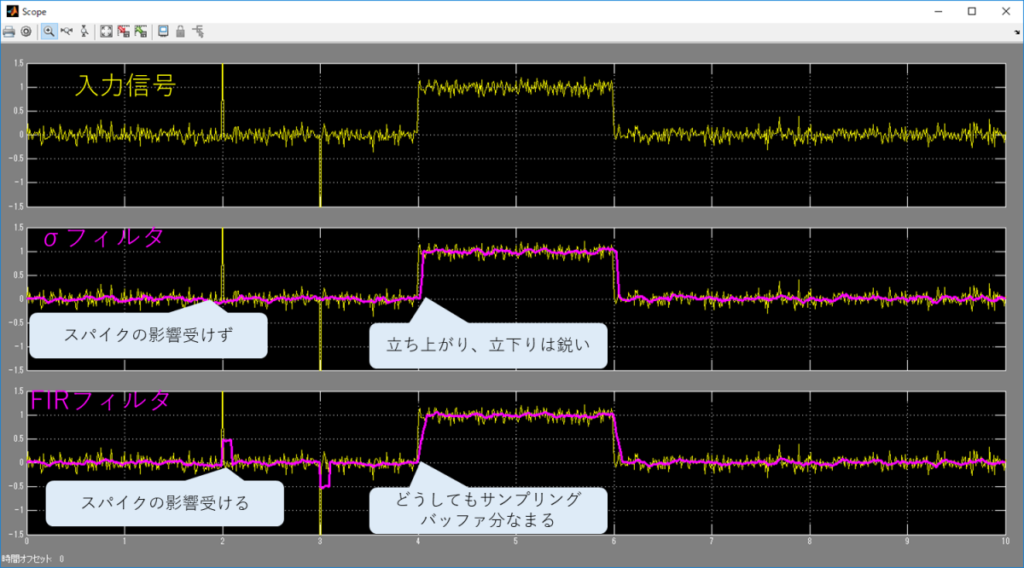

あ、なるほど。
移動平均だと、スパイクノイズが発生した際にしばらく影響が残るんだね。
シグマフィルタはスパイクノイズの影響を受けないし、
立ち上がり、立下りも早いね。

そうそう。
今回はこのフィルタが相性が良いと思う。

うん。
これも仕様書に含めておこう。

これで仕様書としてはOKかな?

そーだね。
また困ったら相談に乗ってよ。

まぁ相談だけならね。

含みのある言い方だなぁ。
まとめ

まとめだよ。
- ノイズは様々な種類があり、設置場所や扱う信号によって異なる。
- 複数のノイズ対策をソフトウェアで実施するとリアルタイム性が犠牲になることがある。
- よって、適切なフィルタアルゴリズムが無いか調べる必要が出てくる。
バックナンバーはこちら




コメント