【やり直し】微分積分についての最低限の復習【高校物理】

はじめに
微分積分と掛け算割り算
$x^n$ の微分と積分
1. $x^n$ の微分(導関数)
2. $x^n$ の(不定)積分(原始関数)
まとめ

はじめに

※ 本記事は以下を親記事とした子記事に該当する。
https://www.simulationroom999.com/blog/mechanics-overview/

力学を学習する上で微分積分を把握しておく必要がある。
しかし、数学的に微分積分を解くということはしないので、とりあえずは雰囲気だけでも押さえておくと良い。
https://ja.wikipedia.org/wiki/%E5%BE%AE%E5%88%86%E7%A9%8D%E5%88%86%E5%AD%A6

微分積分学 - Wikipedia

微分積分と掛け算割り算

古典力学にて、微分積分が大量出てくるが、難しく考える必要は無い。

足し算引き算は計算の初歩
掛け算割り算は計算の基礎
積分微分は計算の原理

である。

変化しないという前提条件を付けると、積分と掛け算は同一であり、微分と割り算と同一である。

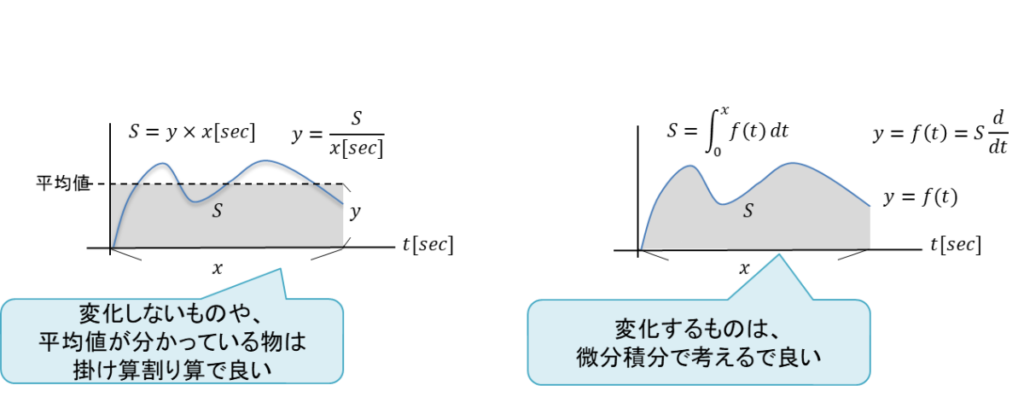
変化しないものや、平均値が分かっている物は掛け算と割り算で良い。変化するものは、微分積分で考えると良い。

要は、概念の段階では掛け算割り算で覚えておいて、
利用するときに対象が変化するものであった時に微分積分に置き換えれば良い。

$x^n$ の微分と積分

$x^n$ の微分と積分に対して一般的なテクニックがある。
力学を学ぶ上で、シレっと当たり前のように書かれていたり使われていたりするので、ここで一度、復習しておく。
(細かい理屈はここはで説明しない。導関数、原始関数でググればたぶん出てくる)

$x^n$ の微分(導関数)

$$x^{\color{red}{n}}\frac{d}{dx}=\color{red}{n}x^{\color{red}{n}-1}$$
例：
$$x^{\color{red}{2}}\frac{d}{dx}=\color{red}{2}x$$
$$(x^{\color{red}{3}}+2x^{\color{red}{2}}+1)\frac{d}{dx}=\color{red}{3}x^{\color{red}{2}}+\color{red}{4}x$$

$x^n$ の(不定)積分(原始関数)

$$\int x^{\color{red}{n}}dx=\frac{1}{\color{red}{n}+1}x^{\color{red}{n}+1}+C$$
例：
$$\int x dx=\frac{1}{\color{red}{2}}x^{\color{red}{2}}+C$$
$$\int (\color{red}{2}x+3) dx=x^{\color{red}{2}}+\color{red}{3}+C$$

(C)は積分定数。
何かしらの定数が居る可能性を指し示す。
・積分定数が入っている式を一般解。
・初期条件を入れて意味のある定数と差し替えた状態を特殊解。
と呼ぶ。