はじめに
自動車関連の制御及び制御対象を理解するには、物理と数学の知識が必要とされることが多い。
しかし、実のところ本当に必要とされるのは、高校物理レベルの力学の範囲でおおよそ十分。
よって、本記事では高校物理の力学についてさっくりと解説する。
発端
社内、社外でいろいろと技術関連の講釈、講義をすることがまぁまぁあるが、とある人からこういうことを言われた。
「○○(私の名前)さんの言ってることはなんとなく分かるけど、やっぱり良くはわからない。たぶん力学を理解できていないんだと思う。」
なるほど。確かに力学の知識が無い状態で聞いても分かるわけがない。
物理学全般になると話がやや大きいが、力学だけであればある程度情報をシュリンクしてまとめられそうである。
思い立ったが吉日的にまとめてみることにした。
尚、ここ言う力学は古典力学ことニュートン力学を指す。
https://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E5%8A%9B%E5%AD%A6

大学入試 漆原晃の 物理基礎・物理[力学・熱力学編]が面白いほどわかる本
大人のための高校物理復習帳 役立つ物理の公式28 (ブルーバックス)
はじめて学ぶ物理学—学問としての高校物理(上)
はじめて学ぶ物理学—学問としての高校物理(下)
ニュートン力学の構成
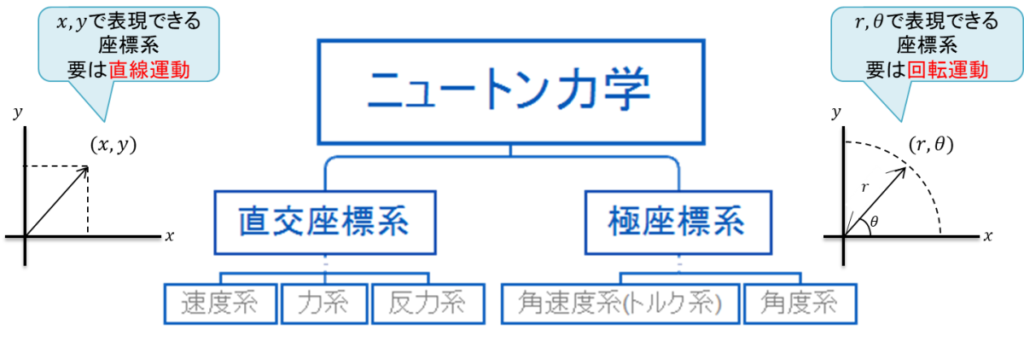
- ニュートン力学をの要素分解
- その上で推奨学習順序を設定
どこから始めてもOKではあるが、どちらにしても直線運動の方がイメージ湧きやすいし、概念もシンプル。
https://www.simulationroom999.com/blog/composition-of-newtonian-mechanics/
微分積分についての最低限の復習
- 力学には微分積分は必須。
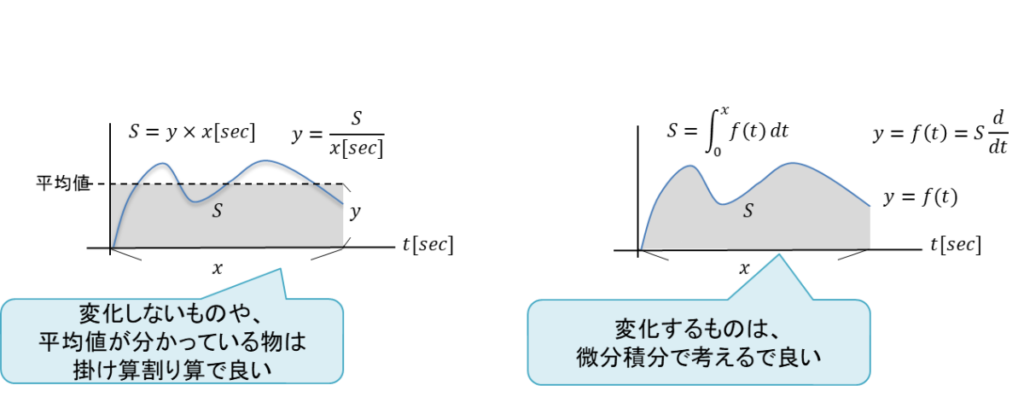
- しかし、難しく考える必要はない。とりあえずは、以下の認識で良い。
- 微分≒割り算
- 積分≒掛け算
- \(x^n\)に対する導関数、原始関数の導出テクニックだけはきっちり押さえておく。
直交座標系
加速度による速度と距離の定義
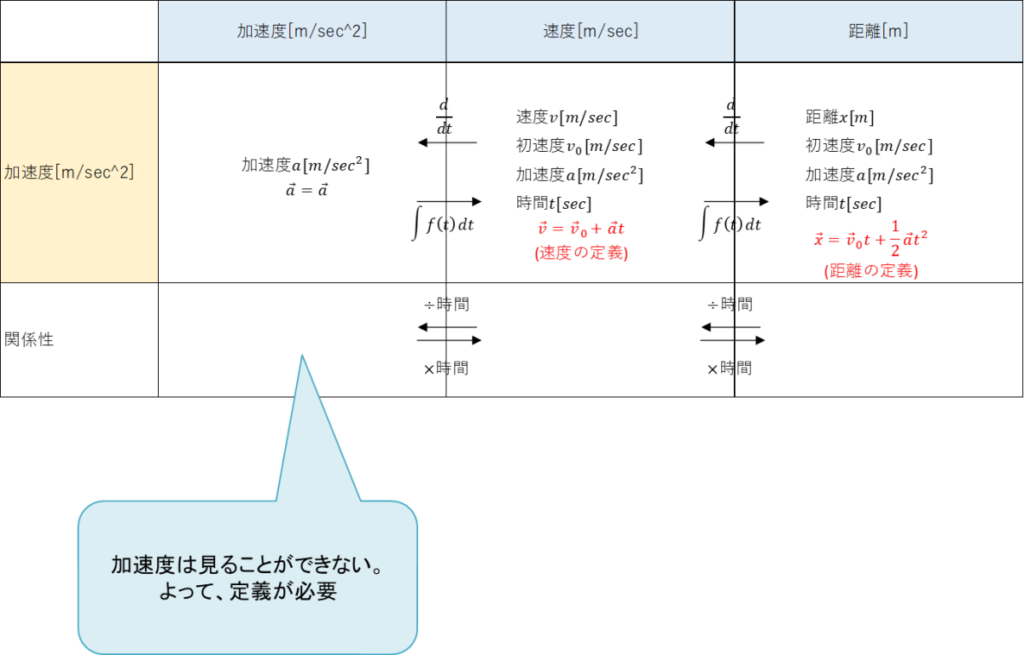
- 加速度と力は密接な関係にある。
- しかし、加速度は人間が見ることができない。
- よって、速度、距離を利用した定義が必要。
- 加速度という概念を用いて、速度と距離を定義することで加速度を定義している。
直線運動(力、運動量、仕事、仕事率)
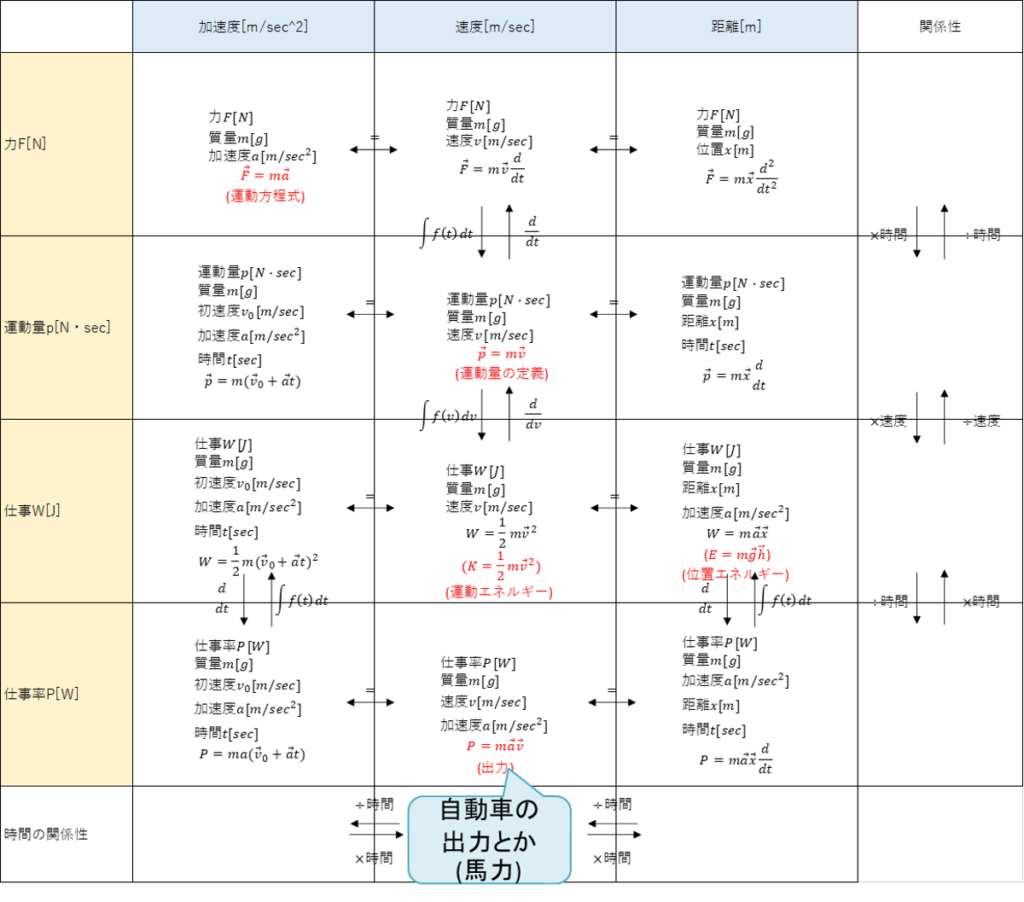
- 力学で登場する定義、公式は加速度-速度-距離と力-運動量-仕事-仕事率をマトリクスで覚えると良い
- 力-運動量-仕事-仕事率の関係性はショートカット可能
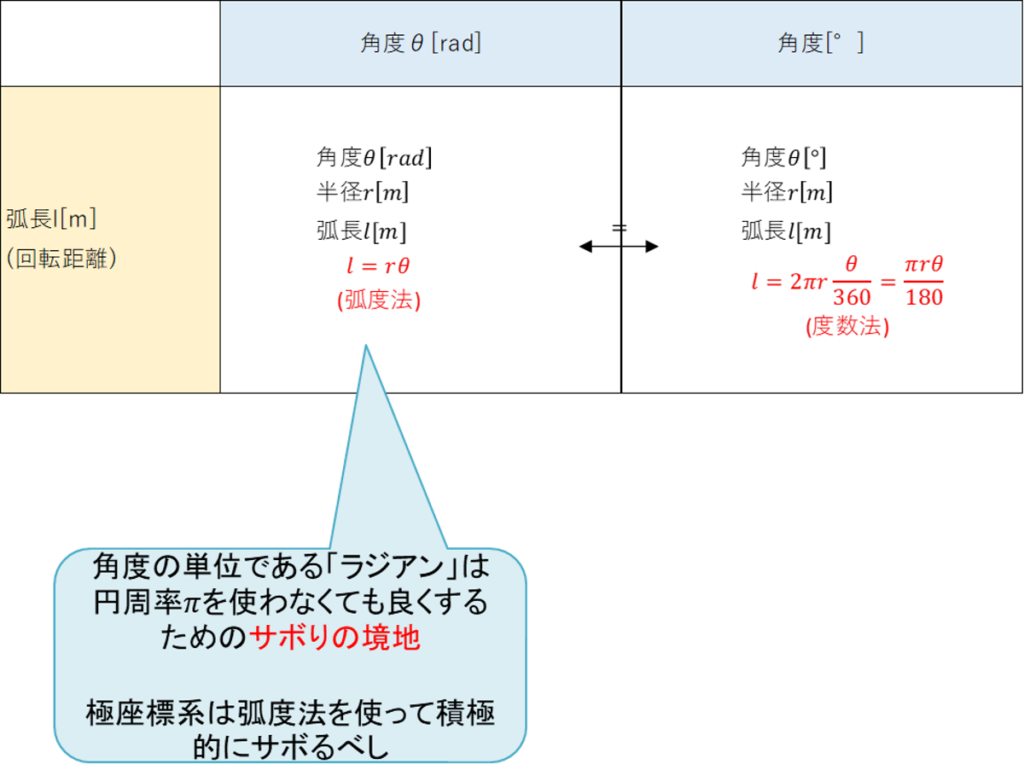
弧度法
回転運動を扱う際は度数法ではなく、弧度法を使って積極的にサボろう。
外積
- 外積をすべて学ぼうとするとまぁまぁなボリュームになる。
- 極座標系に於いては、円周の状態と半径との関係性に使用できる。
- sin関数の関係。

極座標系
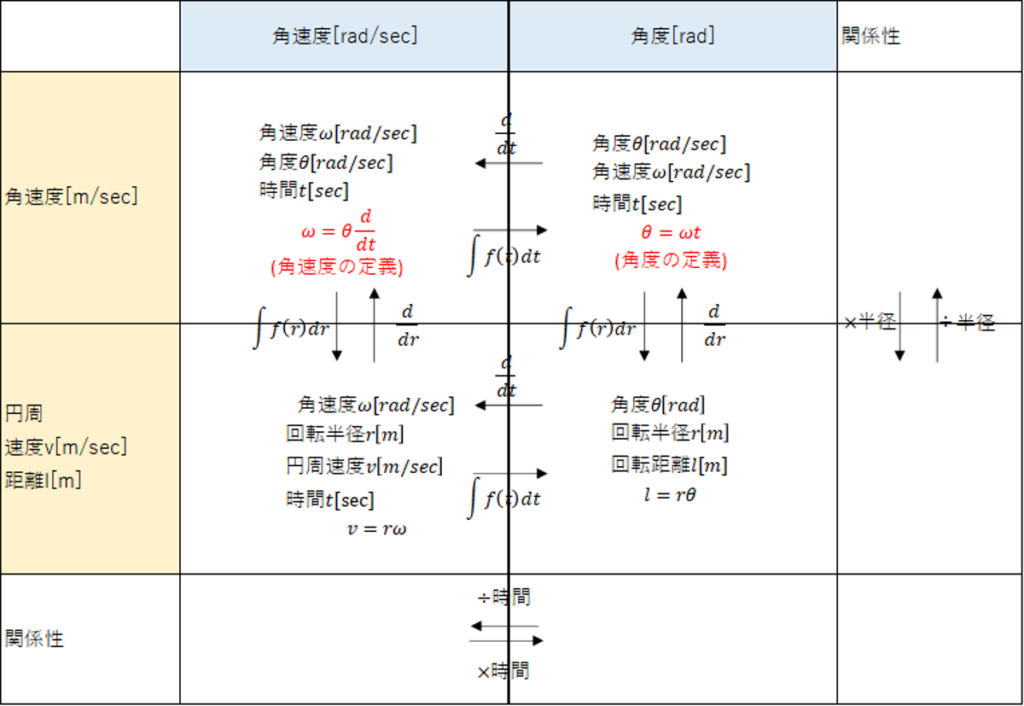
円周と角速度
- 角度=角速度×時間
- 円周=角度×半径
- 弧度法様々
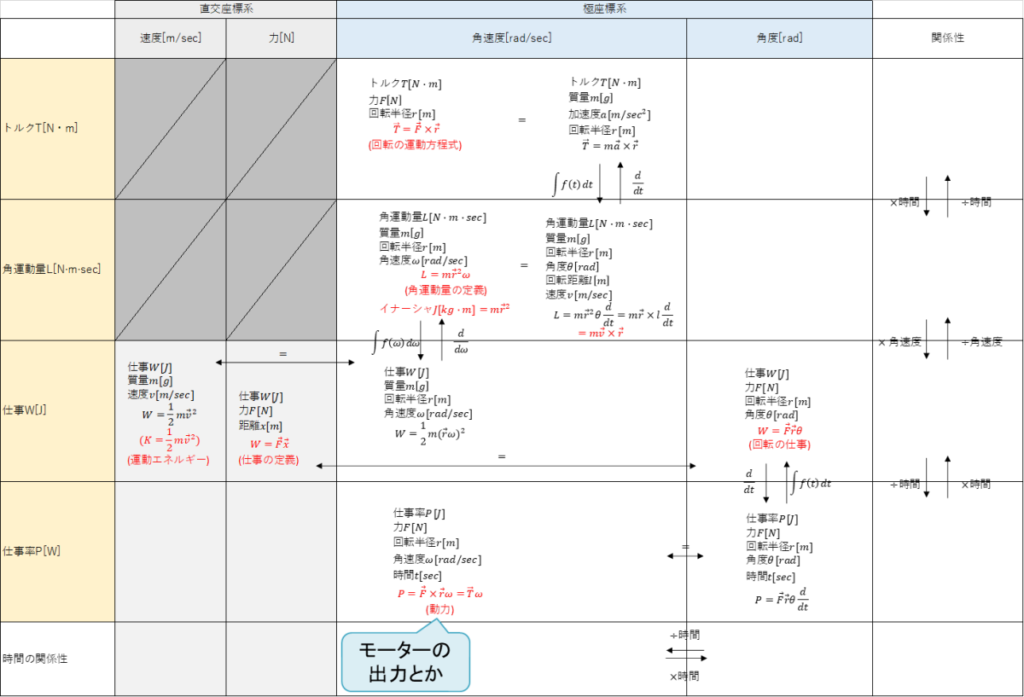
回転運動(トルク、角運動量、仕事、仕事率)
- 回転運動も直線運動に似た各種定義が存在
- トルク、角運動量、仕事、仕事率
- 直交座標と極座標は仕事と仕事率で接続されている
- 角度から円周に概念を移す際は直線運動の向きの概念が入る。
- \(sin(θ)\)の関係 → 外積
- 恐らくこれが混乱の元になっている。
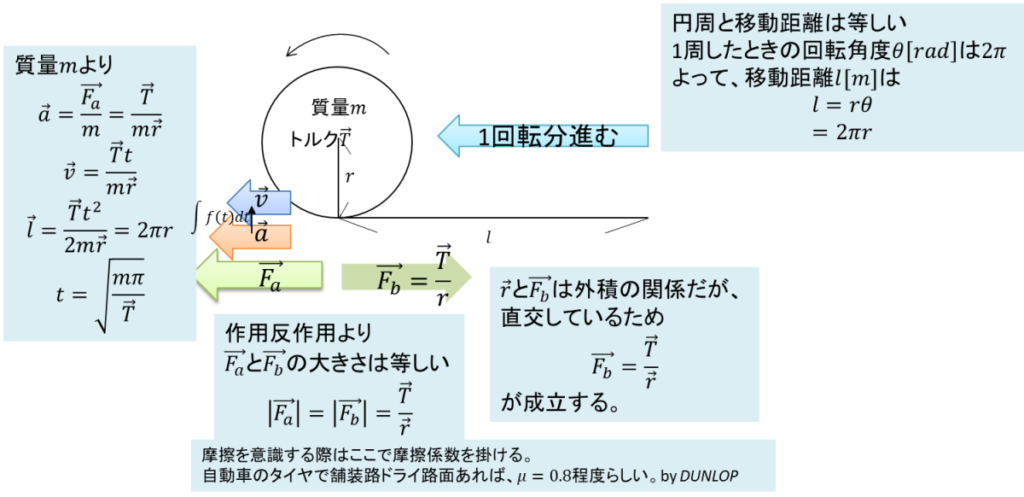
回転運動と直線運動の関係性
- 角度→円周→直線と辿ることで回転運動と直線運動が繋がる。
- 実際は摩擦やイナーシャを意識する必要がある。
まとめ
- 微分積分は割り算/掛け算に置き換えて考えてみる。
- 微分≒割り算。
- 積分≒掛け算。
- 直交座標系力学のポイント。
- 加速度、速度、距離の関係性。
- 力×時間で運動量。
- さらに×速度で仕事。
- それを÷時間で仕事率。
- ショートカットも可能 。
- 力×速度=仕事率。
- 力×距離=仕事。
- 極座標系力学のポイント。
- ラジアンで楽をする。
- 以下を知っていれば、直交座標系の概念がそのまま使える。
- 距離=回転距離
- 速度=角速度×半径
- 直交座標系と極座標系は仕事、仕事率で繋がっている。
- 視点を変えて、自分で勝手な式に作り替えても良い。
- というか、そういう学問。
- 物事を単純なパラメータへばらすテクニックの集大成と捉えても良い。
大学入試 漆原晃の 物理基礎・物理[力学・熱力学編]が面白いほどわかる本
大人のための高校物理復習帳 役立つ物理の公式28 (ブルーバックス)
はじめて学ぶ物理学—学問としての高校物理(上)
はじめて学ぶ物理学—学問としての高校物理(下)











