MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その64【マクローリン展開⑩】
を書き直したもの。
マクローリン展開のおおよその説明をしたところ。
今回は、sin関数のマクローリン展開をScilabで演算しプロットするプログラムを作成
【再掲】sin関数のマクローリン展開
まずは、sin関数のマクローリン展開を再掲。
\(
\begin{eqnarray}
\displaystyle f(x)&=&f(0)+\frac{f^\prime(0)}{1!}x+\frac{f^\prime\prime(0)}{2!}x^2+\dots\\
\displaystyle &=&f(0)+\sum_{n=1}^\infty\frac{f^n(0)}{n!}x^n\\
\displaystyle \sin(x)&=&x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots\\
\displaystyle &=& \sum_{n=0}^\infty\frac{(-1)^n x^{2n+1}}{(2n+1)!}
\end{eqnarray}
\)
今回はScilabでsin関数のマクローリン展開を演算&プロットする。
【再掲】sin関数のマクローリン展開のプログラムフロー
そして、プログラムフローも再掲。
- プロット数、プロット範囲、x軸の定義
- nの次数列を定義
- 次数列に応じて以下を繰り返す
- sin関数のマクローリン級数を演算
- 演算結果をプロット
Scilabコード
Scilabコードは以下。
P=1000; // プロット数
L=2*%pi; // -L~+Lの範囲
x=linspace(-L,L,P); // x軸
Ns = [0,1,2,3,4,5]; // n数セット
K=length(Ns);
for i = 1:K
N=Ns(i); // n数
Maclaurin_series = zeros(1,P);
// Σ(-1)^n x^(2n+1) / (2n+1)!
for n = 0:N
Maclaurin_series = Maclaurin_series + (-1)^n*(x.^(2*n+1))./factorial(2*n+1);
end
subplot(3,ceil(K/3),i );
plot(x,sin(x),'LineWidth',3);
plot(x,Maclaurin_series,'r','LineWidth',2);
title(sprintf('n=%d',N),'fontsize',6,'fontname',4);
p=gca();p.tight_limits(:)="on";
p.data_bounds(:,1)=[-L;L];
p.data_bounds(:,2)=[-1.5;1.5];
xgrid();
end
処理結果
処理結果は以下。
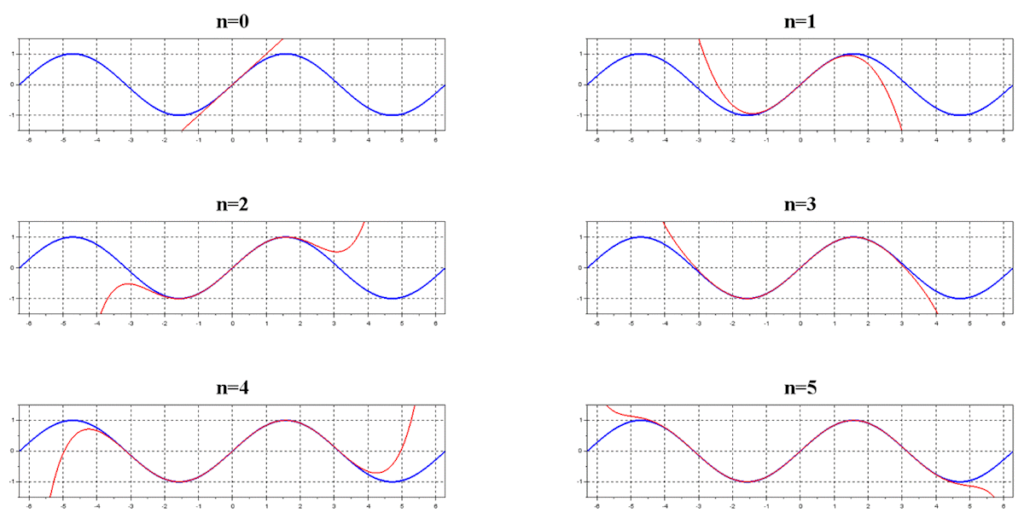
nが増えていけばsin関数になるのが分かるね。
まとめ
- sin関数のマクローリン展開の演算とプロットをScilabで実施。
- nが増えればsin関数に近似していく。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント