sin(x)のマクローリン展開
sin関数のマクローリン展開だが、cos関数と似た感じになる。
見た目上は若干ややこくなるが、ほぼ一緒。
というわけで、sin関数を微分しまくる。
\(
\begin{eqnarray}
f(x)&=&\sin(x)\\
f^{\prime}(x)&=&\cos(x)\\
f^{\prime\prime}(x)&=&-\sin(x)\\
f^{\prime\prime\prime}(x)&=&-\cos(x)\\
f^{\prime\prime\prime\prime}(x)&=&\sin(x)\dots4階微分で\sin(x)に戻る\\
\end{eqnarray}
\)
cos関数の時と似た感じ。
cosの時と同じように整理すると、
\(
f(x)^n=\cases{
\sin(x)\dots(n=0,4,8,\dots)\\
\cos(x)\dots(n=1,5,9,\dots)\\
-\sin(x)\dots(n=2,6,10,\dots)\\
-\cos(x)\dots(n=3,7,11,\dots)\\
}
\)
原点のみで見ると以下になる。
\(
f(0)^n=\cases{
\sin(0)=0\dots(n=0,4,8,\dots)\\
\cos(0)=1\dots(n=1,5,9,\dots)\\
-\sin(0)-0\dots(n=2,6,10,\dots)\\
-\cos(0)=-1\dots(n=3,7,11,\dots)\\
}
\)
nが偶数の時は0になり、奇数の時は符号が反転するので、以下の式にまとめらえる。
\(
\begin{eqnarray}
\displaystyle f(x)&=&f(0)+\frac{f^\prime(0)}{1!}x+\frac{f^\prime\prime(0)}{2!}x^2+\dots\\
\displaystyle &=&f(0)+\sum_{n=1}^\infty\frac{f^n(0)}{n!}x^n\\
\displaystyle \sin(x)&=&x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots\\
\displaystyle &=& \sum_{n=0}^\infty\frac{(-1)^n x^{2n+1}}{(2n+1)!}
\end{eqnarray}
\)
cos関数の時と似てると言えば似てるが、
思ったよりもややこしいことになってはる。
それでも、一つの式で表現できることは重要。
sin関数のマクローリン展開の式を元にプロット
nを徐々に増やした場合のプロットも見せておこう。
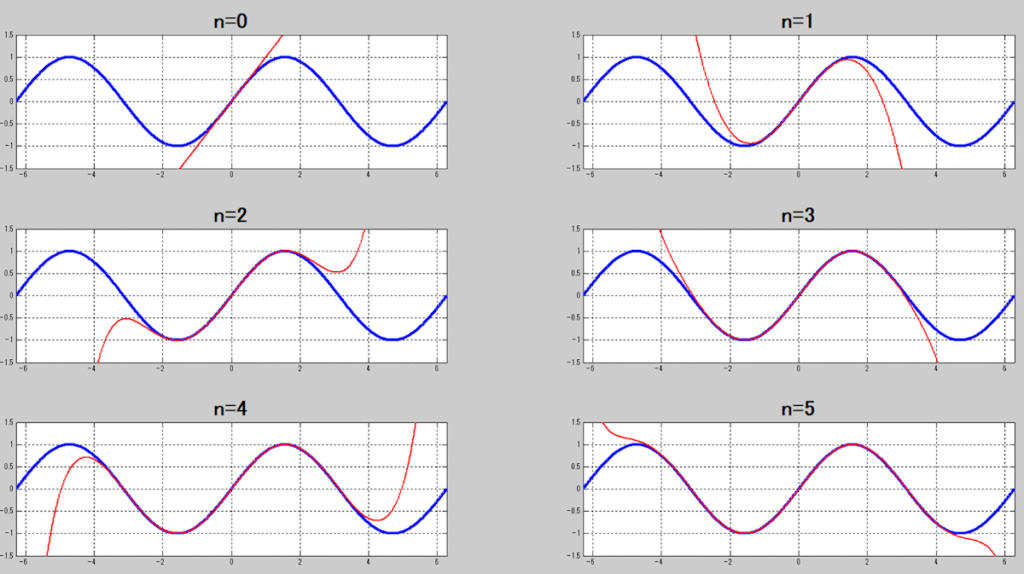
これも徐々に一致する範囲が広がっていく。
無限にやれば、sin関数と同一にはなることがわかるだろう。
まとめ
- cos関数をマクローリン展開。
- cos関数をマクローリン展開したプロットも出してみた。
- sin関数をマクローリン展開。
- sin関数をマクローリン展開したプロットも出してみた。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント