MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その59【マクローリン展開⑤】
MATLAB,Python,Scilab,Julia比較 第5章 その60【マクローリン展開⑥】
を書き直したもの。
前回は指数関数のマクローリン展開の説明。
今回はcos関数とsin関数のマクローリン展開について。
【再掲】複素フーリエ級数に至る道
まずは複素フーリエ級数に至る道を再掲。
- テイラー級数
- マクローリン級数
- 指数関数のマクローリン展開
- cos(x)のマクローリン展開
- sin(x)のマクローリン展開
- オイラーの公式
- 複素フーリエ級数
今回は、cos(x)、sin(x)のマクローリン展開。
cos(x)のマクローリン展開
前回は指数関数だったが、今回はcos関数。
感覚的には指数関数より楽そうなイメージはあるが・・・。
実際のところは指数関数よりもちょっと面倒。
手順は一緒ではあるのだが。
指数関数の時と同じく、
\(\cos(x)\)を微分しまくってみよう。
\(
\begin{eqnarray}
f(x)&=&\cos(x)\\
f^{\prime}(x)&=&-\sin(x)\\
f^{\prime\prime}(x)&=&-\cos(x)\\
f^{\prime\prime\prime}(x)&=&\sin(x)\\
f^{\prime\prime\prime\prime}(x)&=&\cos(x)\dots4階微分で\cos(x)に戻る\\
\end{eqnarray}
\)
指数関数の時よりややこしいことになる・・。
ただ、4階微分で戻るという特性は重要。
一旦整理するとこうなる。
\(
f(x)^n=\cases{
\cos(x)\dots(n=0,4,8,\dots)\\
-\sin(x)\dots(n=1,5,9,\dots)\\
-\cos(x)\dots(n=2,6,10,\dots)\\
\sin(x)\dots(n=3,7,11,\dots)\\
}
\)
一応、パターンみないなのはあるけど、
これを前回みたいな一つの式にまとめるってのはむつかしそうに見える。
が、そうでもない。
さらに、原点の時に限定すると、
\(
f(0)^n=\cases{
\cos(0)=1\dots(n=0,4,8,\dots)\\
-\sin(0)=0\dots(n=1,5,9,\dots)\\
-\cos(0)-1\dots(n=2,6,10,\dots)\\
\sin(0)=0\dots(n=3,7,11,\dots)\\
}
\)
と言う感じで1,0,-1しか出てこない。
nが奇数の時は0になり、偶数の時は符号反転ってことになる。
式として整理すると以下になる。
\(
\begin{eqnarray}
\displaystyle f(x)&=&f(0)+\frac{f^\prime(0)}{1!}x+\frac{f^\prime\prime(0)}{2!}x^2+\dots\\
\displaystyle &=&f(0)+\sum_{n=1}^\infty\frac{f^n(0)}{n!}x^n\\
\displaystyle \cos(x)&=&1-x+\frac{x^2}{2!}-\frac{x^4}{4!}+\frac{x^6}{6!}+\dots\\
\displaystyle &=& \sum_{n=0}^\infty\frac{(-1)^n x^{2n}}{(2n)!}
\end{eqnarray}
\)
0の時は消しちゃって良いから、1と-1の時だけ感がればシンプルになる。
cos関数のマクローリン展開の式を元にプロット
nを徐々に増やした場合のプロットも見せておこう。
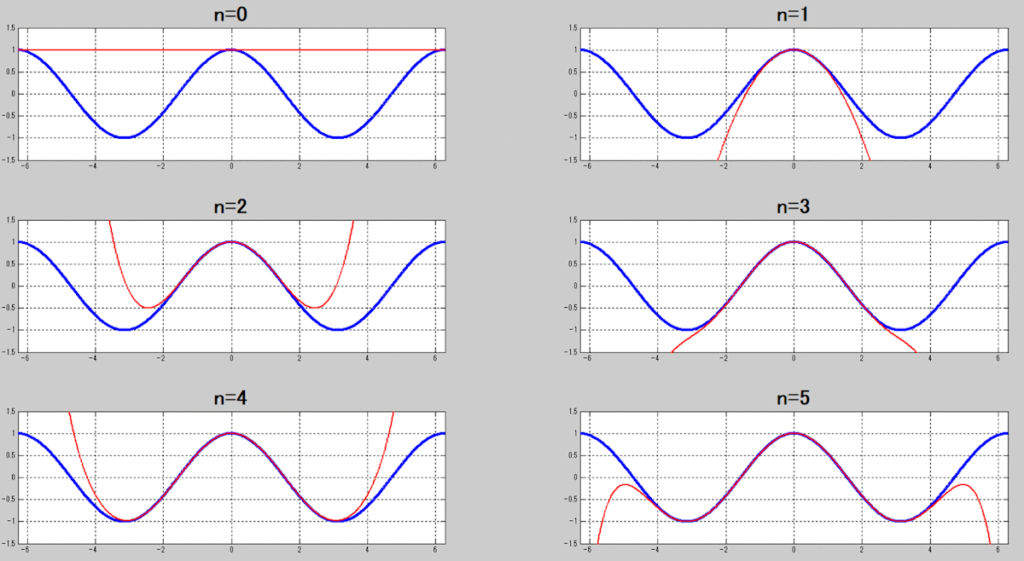
徐々に一致する範囲が広がっていく。
無限にやれば、cos関数と同一にはなりそうというのがわかるだろう。
次のページへ
次のページではcos関数のマクローリン展開について。





コメント