機械学習の手法

はじめに
学習種類
教師あり学習
教師なし学習
教師あり学習の代表的な手法
教師なし学習の代表的な手法
1. k-means
2. 主成分解析(PCA：Principal Component Analysis)
まとめ

はじめに

※ G検定対策ページはこちら。
https://www.simulationroom999.com/blog/jdla-deep-learning-for-general-2020-1/

機械学習の手法は大きく分けて以下となる。

機械学習の手法そのもの
機械学習の評価手法

今回は「機械学習の手法そのもの」について記載する。

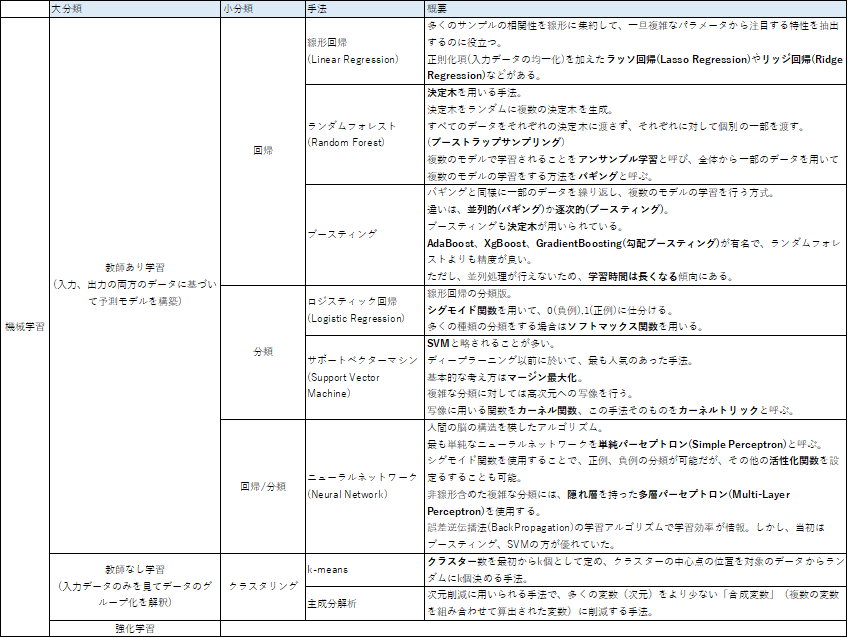
機械学習、教師あり学習、入力、出力の両方のデータに基づいて予測モデルを構築、教師なし学習、入力データのみを見てデータのグループ化を解釈、強化学習、回帰、分類、クラスリング、線形回帰、ランダムフォレスト、ブースティング、ロジスティック回帰、さぽーどベクターマシン、にゅーるらるネットワーク、K-means、主成分解析

学習種類

学習種類は大きく分けて以下。

教師あり学習
教師なし学習
強化学習

教師あり学習

教師あり学習とは以下と定義されている。

与えられたデータ(入力)と元に、そのデータがどんなパターン(出力)になるのかを識別・予測する。

さらに２つに分類される。

回帰問題
- 過去の売上から将来の売上を予測したい。など
分類問題
- 動物の画像を識別したい。など

教師なし学習

教師なし学習は入力と出力がセットとなったデータを用い、出力データがない。
(つまり、教師あり学習と教師なし学習の教師とは出力データを指す)

教師なし学習では主に以下のようなシーンで利用される。

売上データから顧客層の動向を認識したい
入力データの相関性を把握したい

教師あり学習の代表的な手法

線形回帰(Linear Regression)

線形回帰(Linear Regression)は最もシンプルなモデルの一つで、統計でも使用される。
多くのサンプルの相関性を線形に集約して、一旦複雑なパラメータから注目する特性を抽出するのに役立つ。
また、線形回帰に正則化項(入力データの均一化)を加えたラッソ回帰(Lasso Regression)やリッジ回帰(Ridge Regression)などがある。

ロジスティック回帰(Logistic Regression)

線形回帰の分類版として、ロジスティック回帰(Logistic Regression)がある。
シグモイド関数を用いて、0(負例),1(正例)に仕分けるというタイプの分類。
基本的には0.5を閾値として負例、正例と分類するが、この閾値を意図的に0.7や0.3としても良い。

また、シグモイド関数では2値だが、多くの種類の分類をする場合はソフトマックス関数を用いることがある。

ランダムフォレスト(Random Forest)

ランダムフォレスト(Random Forest)は決定木を用いる手法。
決定木は特徴量を逐次評価し、最終的に一つの出力を予測する分岐路を指す。

ランダムフォレストはこの決定木をランダムに複数の決定木を生成する。
また、すべてのデータをそれぞれの決定木に渡さず、それぞれに対して個別の一部を渡す。
(ブーストラップサンプリング)

それぞれの決定木の結果は異なるが、これらの結果で多数決を取ることで最終的な出力を決定する。
決定木の精度が悪くても、集合知で良い精度が得られることを期待したモデルとなる。

ランダムフォレストのように複数のモデルで学習されることをアンサンブル学習と呼び、全体から一部のデータを用いて複数のモデルの学習をする方法をバギングと呼ぶ。

ブースティング(Boosting)

バギングと同様にブースティングも一部のデータを繰り返し、複数のモデルの学習を行う方式。
違いは、並列的(バギング)か逐次的(ブースティング)かにある。
ブースティングでは以下の流れで出力を決定する。

一つのモデルを作成し、学習する。
上記で誤認識したデータを優先的に正しく分類できるように学習
上記2つを繰り返し、最終的に一つのモデルとして出力する

ブースティングも決定木が用いられている。
AdaBoost、XgBoost、GradientBoosting(勾配ブースティング)が有名で、ランダムフォレストよりも精度が良い。
ただし、並列処理が行えないため、学習時間は長くなる傾向にある。

サポートベクターマシン(Support Vector Machine)

サポートベクターマシンはSVMと略されることが多い。
ディープラーニング以前に於いて、最も人気のあった手法。
基本的な考え方はマージン最大化。
マージン最大化とは、各データ点との距離が最大となる境界線でパターン分類を行う手法。
しかし、以下の問題がある。

扱うデータが高次元
線形分類できない

これの対処方法は以下。

高次元に写像
写像後の空間で線形分類

写像に用いる関数をカーネル関数、この手法そのものをカーネルトリックと呼ぶ。

ニューラルネットワーク(Neural Network)

ニューラルネットワークは人間の脳の構造を模したアルゴリズム。
人間の脳はニューロンという神経細胞があるが、これらが結びついて神経回路を構成している。
この神経回路が伝える電気信号で人間の脳はパターンを認識している。

最も単純なニューラルネットワークを単純パーセプトロン(Simple Perceptron)と呼ぶ。
複数の特徴量(入力)から一つの出力を行う。
入力を受け取る部分を入力層、出力する部分を出力層と言う。
入力層のニューロンと出力層のニューロンの繋がりに重みが存在し、
この重みが、どれだけの信号を伝えるかを調整する。
出力が0、1になるようにすることで、正例、負例の分類が可能となる。
上記はシグモイド関数を出力層で使用した場合だが、これ以外の調整関数を設定する事もできる。
この調整関数を活性化関数と呼ぶ。

単純パーセプトロンでは回路が単純すぎるため、複雑な分類が出来ない問題を持つが、
層を追加するアプローチで多層パーセプトロン(Multi-Layer Perceptron)が存在する。

多層パーセプトロンは入力層と出力層の間に隠れ層を追加したものになる。
これにより、非線形含めた複雑な分類を可能にしている。

層が増えることで学習が困難になったが、
誤差逆伝播法(BackPropagation)が考えられたことにより、学習効率が一気に改善された。
しかし、識別・予測の性能はブースティング、SVMの方が優れており、
ディープラーニングが登場する前に於いてのニューラルネットワークはそれほど注目は浴びていなかった。