【入門】分散共分散で最小二乗法(Python)【数値計算】

MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
数式再掲
Pythonコード
実行結果
考察
まとめ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その25【最小二乗法㉔】

を書き直したもの。

平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
Python(Numpy)を使用して算出してみる。

数式再掲

まずは数式を再掲。

\(
\begin{eqnarray}
a&=&\frac{\sigma_{xy}}{\sigma_x^2}\\
b&=&\bar{y}-a\bar{x}
\end{eqnarray}
\)

Pythonコード

そして、Pythonコードは以下になる。

import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])

# 共分散利用
C=np.cov(x,y,ddof=0)
print("共分散行列")
print(C)
print("分散");
print("xの分散=%f" % np.var(x ,ddof=0));
print("yの分散=%f" % np.var(y ,ddof=0));

a=C[0][1]/np.var(x ,ddof=0)
b=np.average(y)-a*np.average(x)
print("各係数 %.15f,%.15f" % (a,b) )

xp = np.linspace(0, 4, 400)	# 同定した1次関数のx軸を生成
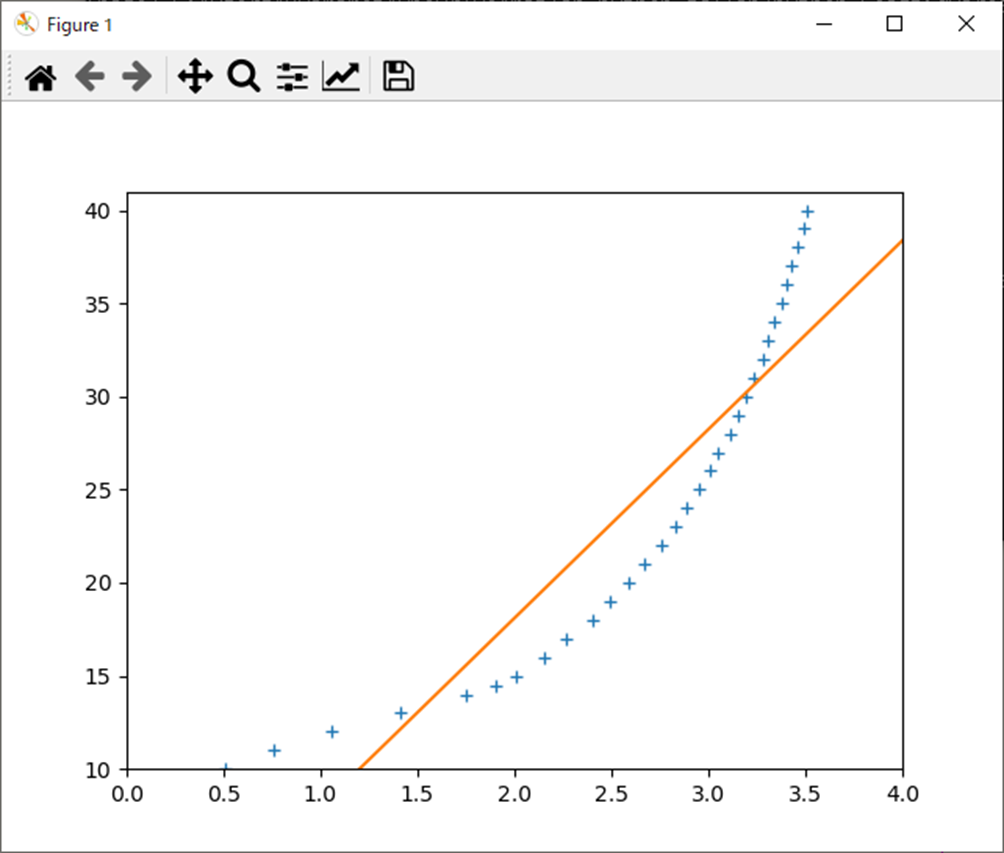
plt.plot(x, y, '+', xp, a*xp+b, '-' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()

実行結果

実行結果は以下。

平均分散共分散による1次関数最小二乗法Python(Numpy)、Figure1

共分散行列
[[ 0.66159023  6.70391602]
 [ 6.70391602 80.83764648]]
分散
xの分散=0.661590
yの分散=80.837646
各係数 10.133033511230929,-2.161664366928406

考察

雰囲気はMATLABと一緒。
ddof=0を指定すると標本分散になる。
covが分散共分散行列を返すところもMATLABと一緒。

\(
\begin{bmatrix}
xの分散 && xyの共分散\\
yxの共分散 && yの分散
\end{bmatrix}
\)

あとはこれといった差は無い。

まとめ

平均分散共分散を使用した一次関数最小二乗法をPython(Numpy)で記載。
- covとvarを使用する。
covは共分散だけでなく、分散共分散行列が取得される。
- よって、covだけでも分散は取得可能。

MATLAB、Python、Scilab、Julia比較ページはこちら