【入門】分散共分散で最小二乗法(Julia)【数値計算】

MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
数式再掲
Juliaコード
実行結果
考察
まとめ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その27【最小二乗法㉖】

を書き直したもの。

平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
Juliaを使用して算出してみる。

数式再掲

今回はJulia。
恒例の数式再掲。

\(
\begin{eqnarray}
a&=&\frac{\sigma_{xy}}{\sigma_x^2}\\
b&=&\bar{y}-a\bar{x}
\end{eqnarray}
\)

Juliaコード

Juliaコードは以下になる。

using PyPlot
using Statistics
using Printf

function LeastSquares_test()
    x=[0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
    y=[10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
    
    # 共分散利用
    c=cov(x,y,corrected=false);
    @printf("共分散:%f\n",c);
    @printf("分散:%f\n",var(x,corrected=false));
    
    # 最小二乗法
    a=c/var(x,corrected=false);
    b=mean(y)-a*mean(x);
    @printf("係数：%.15f, %.15f\n",a,b);
    
    xp = range(0, 4-0.01, step=0.01); # 同定した1次関数のx軸を生成
    plot(x, y, marker="+", linestyle="None" );
    plot(xp, a.*xp.+b );
    ylim([10,41]);
    xlim([0,4]);
    
    return;
end

LeastSquares_test();

実行結果

以下が実行結果

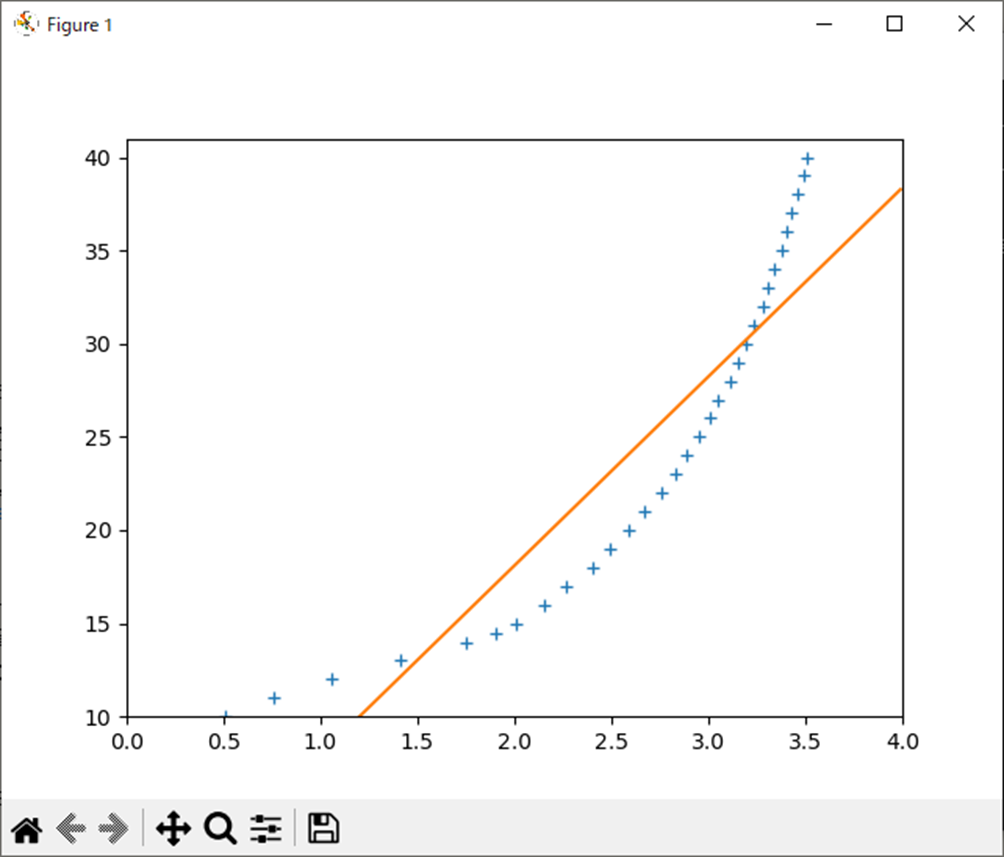
共分散:6.703916
分散:0.661590
係数：10.133033511230929, -2.161664366928402

考察

covとvarを使ってるあたりはMATLABと一緒っぽくは見えるけど、なんか違う。
covの戻り値が行列ではない。
つまり、分散共分散行列ではない。

Juliaでこの使い方をした場合、covは分散共分散行列を返さなくて、共分散のみを返す。
ちなみに、corrected=falseで標本分散、corrected=trueで不偏分散。
デフォルトでは不偏分散。

ちなみに以下のようにすると、Juliaのcovでも分散共分散行列を取得できる。

a=[x y]
cov(a,corrected=false)

結果


 0.66159   6.70392
 6.70392  80.8376

\(
\begin{bmatrix}
xの分散 && xyの共分散\\
yxの共分散 && yの分散
\end{bmatrix}
\)

xとyを2列並べた行列としてcovに渡すと、その2列に対しての分散共分散行列を取得できる。
この書き方はMATLAB、Python(Numpy)、Scilabでも同様。
ただし、Python(Numpy)だけは2列ではなく、2行にする必要はある。

そこらへんは、各ツール、各言語の設計ポリシーみたいなものなのだろう。

まとめ

平均分散共分散を使用した一次関数最小二乗法をJuliaで記載。
- covとvarを使用する。
- covは共分散を返す。
  - MATLABのように分散共分散行列にはなっていない。
  - パラメータを2列に並べて渡すと分散共分散行列を返す。

MATLAB、Python、Scilab、Julia比較ページはこちら