総和
まずは総和。
単純に全部足せばOKってだけになる。
式で表現すると以下。
\(
\displaystyle \sum y_i
\)
ちなみに、暗黙的に\(\displaystyle \sum\)は\(\displaystyle \sum_{i=1}^n\)なんだけど、毎回書くとめんどくさいので省略する。
ここは特に悩むところはないだろう。
そして、今回使う式としては以下のような係数と要素数の積を\(\displaystyle \sum\)で表現できることを明記しておく。
これは重要な式なので後で使う。
\(
\displaystyle a\sum 1 = an
\)
総和と平均の関係
総和がわかると自然と平均もわかる。
総和を要素数で割ればOK。
\(
\displaystyle \bar{y}=\frac{1}{n} \sum y_i
\)
平均値は変数の上にバーを置く書き方をするのが通例となってる。
これを変形すると以下になる。
\(
\displaystyle n\bar{y}=\sum y_i
\)
見てわかる通り、nを左辺から右辺に持ってきただけである。
これも重要な式なので後で使う。
分散の定義
次は分散。
定義は以下になる。
\(
\displaystyle \sigma_x^2=\frac{1}{n}\sum (x_i-\bar{x})^2
\)
分散は\(\sigma_x^2\)みたいな書き方をする。
分散の平方根である標準偏差を\(\sigma_x\)として示す。
分散の方は標準偏差から見たら2乗されたものとして\(\sigma_x^2\)と表現されるのだろう。
分散の式の変形
これも変形する。
変形式の方が重要で、あとで使う。
\(
\begin{eqnarray}
\displaystyle \sigma_x^2 &=& \frac{1}{n}\sum (x_i-\bar{x})^2 \\
\displaystyle &=& \frac{1}{n}\sum(x_i^2-2x_i \bar{x}+(\bar{x})^2) \\
\displaystyle &=& \frac{1}{n}\sum x_i^2 + \frac{2\bar{x}}{n}\sum x_i + \frac{(\bar{x})^2}{n}\sum 1\\
\displaystyle &=& \bar{x_i^2}-2\bar{x}\bar{x}+\frac{n}{n}(\bar{x})^2\\
&=&\bar{x_i^2}-2(\bar{x})^2+(\bar{x})^2\\
&=&\bar{x_i^2}-(\bar{x})^2
\end{eqnarray}
\)
計算過程は複雑だが、最終的にはシンプルになる。
\(\displaystyle \sum\)が居ても、同じように展開できるのと
各項の総和に書き直しても分配が成立できるというのがポイント。
分配ができるというのがイメージできない場合は、Excelの方をイメージしてもらうと良いかもしれない。
表全体を一気に合計するのと、
1列ずつ合計したものに対して合計したもの。
結果は一緒になるだろう。
共分散
共分散は分かりにくい概念である。
まずはWikipediaを引用しよう。
共分散(きょうぶんさん、英: covariance)とは、大きさが同じ2つのデータの間での、平均からの偏差の積の平均値である
Wikipediaより(https://ja.wikipedia.org/wiki/%E5%85%B1%E5%88%86%E6%95%A3)
これを見ても何もわからないかもしれない。
このWikipediaのページに例が載ってるのだが、それを見た方が良いかもしれない。
2つのデータの相関性を評価するためのものと思えばOK。
共分散の性質
- 0ならば2つのデータの間に相関は無い
- 正ならば、2つのデータの間に正の相関があり、値が大きい方がより強い相関になる。
- 負ならば、2つのデータの間に負の相関があり、値が大きい方がより強い相関になる。
相関
さらに相関と言われてもピンと来ない人もいるかもしれないので簡単に説明。
ざっと描くとこんな感じ。
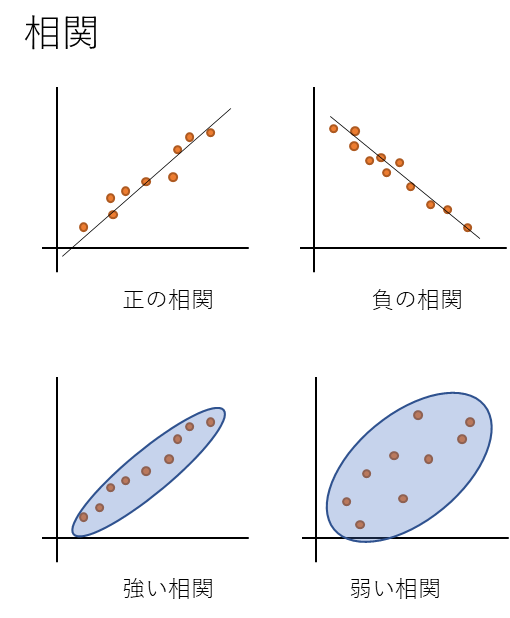
なんとなく最小二乗法との関係性についても感じ取れたのではなかろうか?
共分散の基本公式と変形式
共分散の基本公式と変形式を出そう。
これも最後の変形式が重要な式となる。
\(
\begin{eqnarray}
\displaystyle \sigma_{xy}&=&\frac{1}{n}\sum(x_i-\bar{x})(y_i-\bar{y})\dots基本公式 \\
&=&\frac{1}{n}\sum(x_i y_i-\bar{x}y_i-x_i\bar{y}+\bar{x}\bar{y}) \\
&=&\frac{1}{n}\sum x_i y_i – \frac{\bar{x}}{n}\sum y_i – \frac{\bar{y}}{n}\sum x_i+\frac{\bar{x}\bar{y}}{n}\sum 1\\
&=&\frac{1}{n}\sum x_i y_i – \bar{x}{\color{red}{\frac{1}{n}\sum y_i}} – \bar{y}{\color{red}{\frac{1}{n}\sum x_i}}+\bar{x}\bar{y}{\color{red}{\frac{1}{n}\sum 1}}\\
&=&\frac{1}{n}\sum x_i y_i – \bar{x}\bar{y}-\bar{y}\bar{x}+\bar{x}\bar{y}\\
&=&\frac{1}{n}\sum x_i y_i – \bar{x}\bar{y}
\end{eqnarray}
\)
これも途中式は複雑だが、最終的にはシンプルになる。
ポイントは赤文字にしている部分。
これは平均の公式と一緒。
これの影響でシンプルになってる。
これで、1次関数の最小二乗法に対する変形の準備が整ったところ。


コメント