【入門】最小二乗法(Julia)【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
Juliaによる1次関数の最小二乗法
Juliaコード
実行結果
まとめ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その11【最小二乗法⑩】

を書き直したもの。

最小二乗法をJuliaを使って解いてみる話。

Juliaによる1次関数の最小二乗法

Juliaが一番慣れてないから、どうなるかが読みずらい。

結論としては
Polynomialsパッケージのfit関数で解くことができる。

Polynomialsが多項式という意味で、
それのfit関数だから、
MATLAB,PythonのNumpyのpolyfitに近い表現ともいえる。

というわけで、使い方としては似ている。
しかし、根本的に異なっている部分もあるので注意。

今回に於いては大した問題ではないが、
取得できるのが係数じゃなくて関数になる。
関数そのものを参照できるから、係数の確認はできる。
むしろ、今回の目的からすると関数のままplotに渡せばOKだから、楽になったと言える。

これは実際のコードを見てもらった方が早い。

Juliaコード

Juliaコードは以下になる。

using Polynomials
using PyPlot

x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
func = fit(x, y,1);
print("各係数")
print(func)
xp=Vector(0:1/400:4);
plot(x, y, "+" );
plot(xp, func.(xp) );
ylim([10,41]);
xlim([0,4]);

実行結果

実行結果は以下になる。

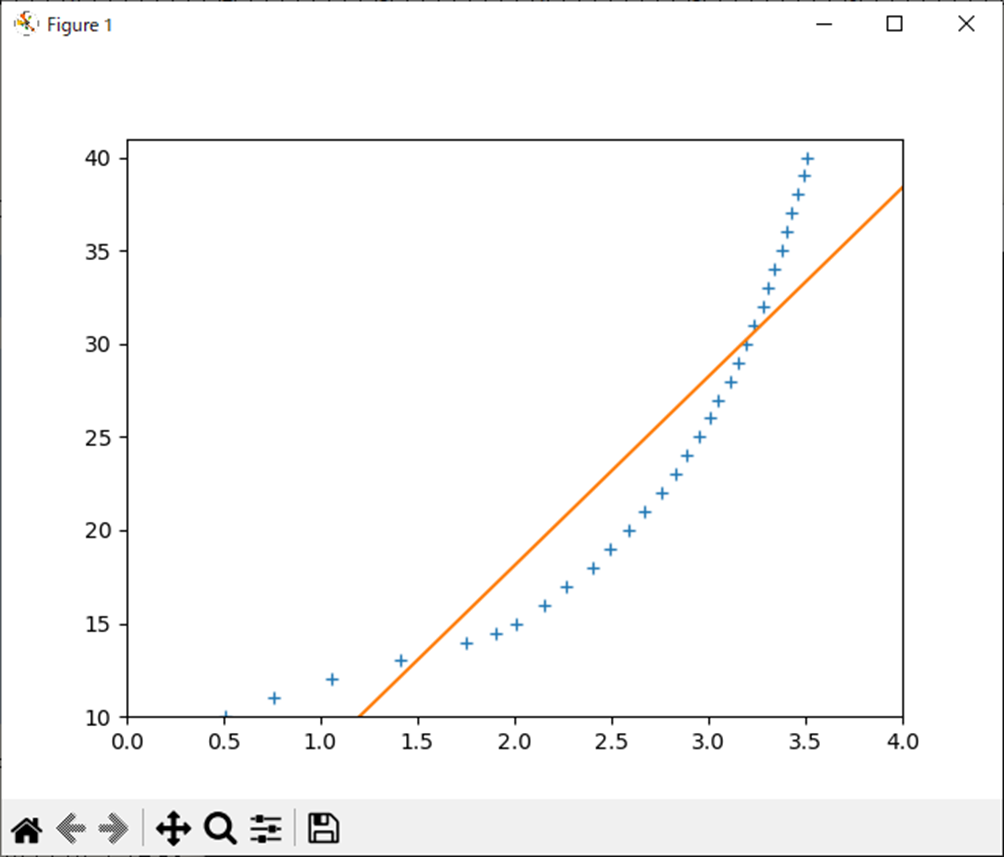
各係数
-2.16166 + 10.133*x

各係数が関数そのものを示している。
ここがMATLAB、PythonのNumpyのpolyfitを大きく異なる点。

係数単体の値が欲しい場合は以下のように取得できる。

julia> func[0]
-2.161664366928408

julia> func[1]
10.133033511230932

よって、便利にはなれど、不都合になることは無いと思われる。

まとめ

Juliaにて1次関数の最小二乗法を実施。
- Polynomialsパッケージのfit関数を使用。
- 他のツール、言語と異なり、係数ではなく、関数が取得される。
- 配列としてアクセスすれば、係数単体の値と取得できる。

MATLAB、Python、Scilab、Julia比較ページはこちら